Graf funkce
Graf funkce

Teoretické minimum
Grafem funkce @if@i rozumíme množinu uspořádaných dvojic reálných čísel @b\mathrm{graf} (f)=\left\lbrace (x,f(x))\in\mathbb{R}^2\, |\, x \in D(f)\right\rbrace,@b
kterou znázorňujeme v rovině @i x,\, y@i tak, že hodnotu nezávisle proměnné nanášíme na vodorovnou osu @i x@i a hodnotu závisle proměnné na svislou osu @i y@i. V rovině @i x,\, y@i pak vyneseme body o souřadnicích @i (x,f(x))@i, kde @i x\in D(f)@i. Užitečná poznámka: Uvědomte si, že musí platit:
- Definiční obor @i D(f)@i je vždy kolmý průmět grafu @i f@i na osu @i x@i.
- Obor hodnot @i H(f)@i je vždy kolmý průmět grafu @i f@i na osu @i y@i.

Mějme dán graf funkce @i f@i. Funkční hodnotu @i f(x_1)@i pro dané @ix_1@i určíme tak, že @ix_1@i promítneme svisle na graf do bodu @i(x_1,f(x_1))@i, potom @iy@i-ová souřadnice tohoto bodu je hledaná funkční hodnota @i f(x_1)@i, viz následující
obrázek.
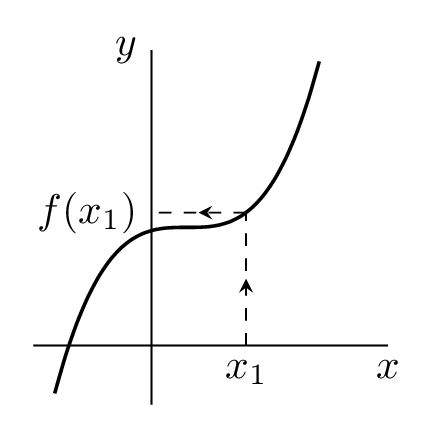
Hledáme-li naopak vzor bodu @iy_0@i, postupujeme opačně. Jedna hodnota @iy_0@i může mít obecně více vzorů. Pro funkci na následujícím obrázku například platí, že @if(x_1)=f(x_2)=y_0@i.

Podobně zjišťujeme, jak se při zadané funkci @i f@i zobrazí celý interval. To budeme potřebovat zejména v kapitolách Operace s funkcemi a Funkce prosté a funkce k nim inverzní.
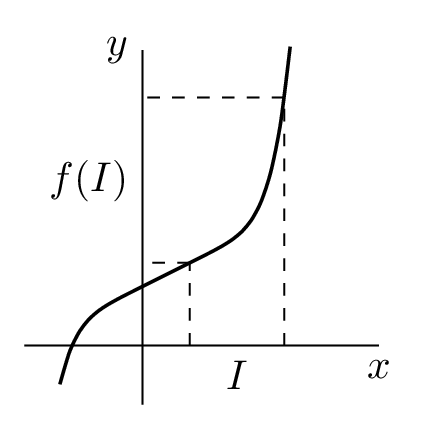
Známe-li graf nějaké funkce, lze z něj v podstatě ,,vyčíst" všechny její důležité vlastnosti. Naopak, máme-li funkci zadanou nějakým předpisem, bývá často naším cílem nakreslit její graf.
Pod pojmem elementární funkce rozumíme pro naše potřeby funkce uvedené v Tabulce I ze skript Matematika I, která je přílohou této kapitoly. Jedná se zejména o funkce lineární, mocninné, odmocninové, lomené, exponenciální, logaritmické, goniometrické, cyklometrické, dále o funkce signum a absolutní hodnota. Pro úspěšné zvládnutí učiva tohoto kurzu je nutná výborná znalost grafů těchto funkcí a jejich základních vlastností.
V následujícím si ukážeme, jak načrtnout grafy funkcí, které se získají z elementárních funkcí jednoduchými úpravami jako je přičtení konstanty, vynásobení konstantou a podobně. Hovoříme o jednoduchých transformacích grafu. Otázkou, jak načrtnout graf složitější funkce, se pak zabývá kapitola Průběh funkce.
Při črtání grafů funkcí zaznačíme do souřadného systému kromě grafu samotného také význačné body a asymptoty; například vrchol a dva další body pro parabolu či absolutní hodnotu, jeden význačný bod a asymptoty pro hyperbolu, exponenciální a logaritmickou funkci apod. Místo význačných bodů můžeme vyznačit také průsečíky s osami. U periodických funkcí črtáme alespoň dvě opakování základní periody.
Základní transformace grafu
Přičítání konstanty
Známe-li graf funkce @if(x)@i, chceme načrtnout grafy funkcí @if(x)+C@i a @if(x+C)@i, kde @iC \in \mathbb{R}@i je libovolná reálná konstanta.
Tuto transformaci si budeme ilustrovat na příkladu funkce @if(x)=x^2@i.
- Chceme-li načrtnout graf funkce @ig(x)=x^2+2@i, uvědomíme si, že funkční hodnoty @ig(x)@i pro všechna @ix \in D(f)@i vzniknou z hodnoty @if(x)@i zvýšením o dvě. To má za následek posunutí grafu ve svislém směru o dvě nahoru.
- Podobně budeme chtít načrtnut graf funkce @ih(x)=(x-2)^2@i. Zatímco graf funkce @if(x)=x^2@i (parabola) má vrchol v bodě @i(0,0)@i, graf funkce @ih(x)=(x-2)^2@i (opět parabola) má vrchol v bodě @i(2,0)@i. Podobnou úvahu lze provést pro každý další bod na grafu @ih(x)@i. Celkově tedy graf funkce @ih@i vznikne z grafu @if@i posunutím ve vodorovném směru o dvě doprava.

Změna znaménka
Známe-li graf funkce @if(x)@i, chceme načrtnout grafy funkcí @i-f(x)@i a @if(-x)@i.
Tuto jednoduchou změnu si budeme si ilustrovat na funkci @if(x)=\sqrt{x}@i. Všimněme si nejprve, že funkce @if@i je definová pro všechna nezáporná @ix@i a také její funkční hodnoty jsou nezáporné.
- Uvažme nyní funkci @ig(x)=-\sqrt{x}@i. Pro všechna @ix \in D(f)=D(g)@i jsou funkční hodnoty @ig(x)@i opačné k hodnotám @if(x)@i. Není težké si uvědomit, že graf funkce @ig@i vznikne z grafu @if@i překlopením
vzhledem k ose @ix@i.
- Naopak při črtnání grafu funkce @ih(x)=\sqrt{-x}@i si musíme uvědomit, že se nejprve mění znaménko u @ix@i a následně potom odmocňujeme. Funkce @ih(x)=\sqrt{-x}@i přiřadí libovolnému zápornému číslu @i-x \in D(h)@i stejnou
hodnotu jako původní funkce @if@i kladnému číslu @ix \in D(f)@i. Graf funkce @ih@i tedy vznikne z grafu @if@i překlopením vzhledem k ose @iy@i.

Násobení konstantou
Známe-li graf funkce @if(x)@i, chceme načrtnout grafy funkcí @i K f(x)@i a @if(Kx)@i, kde @iK>0@i je nějaká kladná konstanta.
Tyto
transformace si budeme ilustrovat na příkladu funkce
@if(x)=\sin{x}@i.
- Uvažme nejprve funkci @ig(x)=3\sin{x}@i. Pro všechna @ix \in D(f)=D(g)@i jsou funkční hodnoty @ig(x)@i trojnásobné vůči hodnotám @if(x)@i. Zatímco hodnoty funkce @if(x)=\sin{x}@i oscilují mezi @i-1@i a @i+1@i , hodnoty funkce @ig(x)=3\sin{x}@i oscilují mezi @i-3@i a @i+3@i . Také vidíme, že @iH(f)=[-1,1]@i a @iH(g)=[-3,3]@i. Graf funkce @ig@i vznikne tedy z grafu @if@i jeho (trojnásobným) natažením ve směru osy @iy@i .
- Nyní se pokusme načrtnout graf funkce @ih(x)=\sin{\frac x2}@i. Abychom získali představu o chování funkce @ih@i, zkusme si nejprve spočítat několik jejích význačných hodnot. Například @ih(0)=\sin{0}=0,@i
@ih(\frac{\pi}2)=\sin{\frac {\pi}4}=\frac{\sqrt{2}}2,@i
@ih(\pi)=\sin{\frac {\pi}2}=1,@i
@ih(2\pi)=\sin{\pi}=0.@i
Vidíme, že funkce @ih@i
kmitá dvakrát pomaleji než funkce @if@i
.
Zatímco @if(x)=\sin{x}@i
je @i2{\pi}@i-periodická funkce, funkce @ih(x)=\sin{\frac x2}@i
má primitivní periodu @i4{\pi}@i
, viz Vlastnosti funkcí. Graf funkce @ih@i tedy vznikne
grafu @if@i
jeho (dvojnásobným) natažením ve směru osy @ix@i
.

Absolutní hodnota
Známe-li graf funkce @if(x)@i, chceme načrtnout grafy funkcí @i|f(x)|@i a @if(|x|)@i
Funkce absolutní hodnota je definována jako @b|x|=\begin{cases} x,\quad x\ge0\\ -x,\quad x<0.\end{cases}@b
Uvažme libovolnou funkci @if(x)@i.
- Zkusme nejprve načrtnout graf funkce @ig(x)=|f(x)|@i. Pokud je @if(x)>0@i, pak @ig(x)=f(x)@i . Pokud je @if(x)<0@i, pak @ig(x)=-f(x)@i . Tedy ta část grafu @if@i , která leží pod osou @ix@i , se vzhledem k ose @ix@i překlopí (nahoru) , zbytek grafu @if@i zůstává nezměněn.

- Nyní chceme načrtnout graf funkce @ih(x)=f(|x|)@i. Nejprve si uvědomíme, že pro kladná @ix@i je @ih(x)=f(x)@i. Naopak pro záporná @ix@i je @ih(x)=f(-x)@i.
To se na grafu funkce @ih@iprojeví následovně:
napravo od osy @iy@i jsou grafy funkcí @if@ia @ih@i
totožné. Levá část grafu funkce @ih@i
vznikne překlopením pravé části grafu vzhledem k ose @iy@i doleva. Jinak řečeno, graf funkce @ih(x)=f(|x|)@i je vždy symetrický podle osy @iy@i, protože @ih(x)=f(|x|)@i je vždy sudá funkce, viz Vlastnosti funkcí.

@b\mathrm{e}^{|x|}=\begin{cases}\mathrm{e}^x,\quad x\ge0,\\ \mathrm{e}^{-x}=\left(\frac{1}{\mathrm{e}}\right)^x,\quad x<0.\end{cases}@b
Na závěr si shrneme odvozené poznatky pro transformace grafů do následujícího přehledu.
- @i f(x) + C @i : graf @i f@i se posune ve směru osy @i y@i o hodnotu konstanty @iC@i (tedy v kladném směru osy @iy@i pro @iC>0@i, v záporném směru pro @iC<0@i)
- @i f\left( x+C\right)@i: graf @i f@ise posune ve směru osy @ix@i o hodnotu @i-C@i (tedy v kladném směru osy @ix@i pro @iC<0@i, v záporném směru pro @iC>0@i)
- @i-f(x)@i: graf @i f@i se překlopí vzhledem k ose @ix@i
- @if(-x)@i: graf @i f@i se překlopí vzhledem k ose @iy@i
- @iKf(x)@i: je-li @iK>1@i graf @i f@i se rozšíří ve směru osy @iy@i, je-li @i0<K<1@i graf @i f@i se zúží ve směru osy @iy@i
- @if(Kx)@i: je-li @iK>1@i graf @i f@i se zúží ve směru osy @ix@i, je-li @i0<K<1@i graf @i f@i se rozšíří ve směru osy @i x@i
- @i|f(x)|@i: část grafu @i f@i ležící pod osou @ix@i se překlopí vzhledem k ose @ix@i, zbytek grafu se nemění
- @if(|x|)@i: část grafu @i f@i ležící vlevo od osy @iy@i je nahrazena překlopením části ležící vpravo od osy @iy@i vzhledem k ose @iy@i
Zde @iC \in \mathbb{R}@i je libovolná reálná konstanta, @iK>0@i je libovolná kladná konstanta. Navíc předpokládáme, že výrazy @ix+C,-x,Kx@i a @i|x|@i leží v definičním oboru funkce @if@i.
Při více změnách funkce provádíme transformace grafu postupně. Ve výsledném grafu znázorníme všechny důležité hodnoty @i x@i a @i y@i a případně také asymptoty grafu.
Související
Funkce, definiční obor funkce, průběh funkce.
Řešené příklady
1. Načrtněte graf funkce @if(x)=(x+1)^3-2@i.
Vyjdeme z elemetární funkce @if_1(x)=x^3@i a postupnými transformacemi ji převedeme na funkci @if(x)=(x+1)^3-2@i, jejíž graf chceme načrtnout. Graf pomocné funkce @if_2(x)=(x+1)^3@i je vůči grafu @if_1(x)=x^3@i posunutý ve směru osy @ix@i v záporném směru o 1. Graf funkce @if(x)=(x+1)^3-2@i získáme z grafu @if_2(x)=(x+1)^3@i posunutím ve směru osy @iy@i v záporném směru o 2. Pro kontrolu vyznačíme ještě několik význačných bodů grafu @if@i. Body @i(-1,-1),(0,0)@i a @i(1,1)@i se těmito transformacemi přemění na @i(-2,-3),(-1,-2)@i a @i(0,-1)@i.
Pozor, častá chyba: Při črtání si dáváme pozor, aby části grafu směřující do nekonečna zřetelně směřovaly šikmo doleva, resp. doprava, aby nám nevznikla svislá čára. Takto načrtnutý graf by nebyl grafem funkce, protože by jedné hodnotě @ix@i bylo přiřazeno nekonečně mnoho hodnot @iy@i.

2. Načrtněte graf funkce @if(x)=1-2\sqrt{1-x}@i.
Při črtání vyjdeme ze základní funkce @i f_1(x)=\sqrt{x}@i. Postupně pomocí jednoduchých tranformací budme črtat grafy funkcí @i f_2(x)=\sqrt{-x}@i, @i f_3(x)=\sqrt{1-x}=\sqrt{-(x-1)}@i, @i f_4(x)=2\sqrt{1-x}@i, @i f_5(x)=-2\sqrt{1-x}@i a @i f(x)=f_6(x)=1-2\sqrt{1-x}@i. Graf @i f_2@i vznikne překlopením grafu @i f_1@i kolem osy @iy@i. Graf @i f_3@i vznikne posunutím grafu @i f_2@i ve směru osy @ix@i o @i1@i doprava. Graf @i f_4@i se podobá grafu @i f_3@i, ale @i f_4(0)=2@i, zatímco @i f_3(0)=1@i. Graf @i f_5@i vznikne překlopením grafu @i f_4@i kolem osy @ix@i. A nakonec, graf @if= f_6@i vznikne posunutím grafu @i f_5@i ve směru osy @iy@i o @i1@i nahoru.
Pro kontrolu ještě určíme přirozený definiční obor funkce @if@i, @iD(f)=(-\infty,1]@i. Pravoúhlý průmět našeho grafu @if@i tedy musí být interval @i(-\infty,1]@i. Na závěr ještě naznačíme v grafu @if@i význačné hodnoty, body @i(0,0)@i a @i(1,1)@i se změní na @i(1,1)@i a @i(0,-1)@i.

3. Načrtněte graf funkce @if(x)=\frac{1}{x-1}+2@i.
Vyjdeme z elementární funkce @if_1(x)=\frac{1}{x}@i, jejímž grafem je hyperbola. Postupně načrtneme grafy funkcí @if_2(x)=\frac{1}{x-1}@i a @if(x)=f_3(x)=\frac{1}{x-1}+2@i. Graf @i f_2@i vznikne posunutím grafu @i f_1@i ve směru osy @ix@i o @i1@i doprava. Graf @i f_3@i vznikne posunutím grafu @i f_2@i ve směru osy @iy@i o @i2@i nahoru. Posunutí vyznačíme jednak zakreslením význačných bodů, jednak posunutím asymptot grafu funkce. Původní graf funkce @if_1(x)=\frac{1}{x}@i se přibližuje k souřadnicovým osám, posunutý graf funkce @i f@i se blíží k přímkám @ix=1@i a @iy=2@i. Graf @i f@i asymptoty neprotíná, pouze se k nim blíží.

4. Načrtněte graf funkce @if(x)=1+\sin 2x@i.
Vyjdeme z grafu funkce @i f_1(x)=\sin x@i. Postupně načrtneme grafy funkcí @if_2(x)=\sin 2x@i a @if(x)=f_3(x)=1+\sin 2x@i. Graf @i f_2@i vznikne dvojnásobným zúžením grafu @i f_1@i ve směru osy @ix@i. Funkce @i f_1(x)=\sin x@i je @i2{\pi}@i-periodická funkce, zatímco funkce @i f_2(x)=\sin 2x@i je @i{\pi}@i-periodická
. Funkce @i f_2(x)=\sin 2x@i tedy kmitá dvakrát rychleji než @i f_1(x)=\sin x@i.
Pro kontrolu můžeme spočítat několik význačných hodnot funkce @i f_2(x)@i.
Graf @i f_3@i vznikne posunutím grafu @i f_2@i ve směru osy @iy@i o @i1@i nahoru.

5. Načrtněte graf funkce @if(x)=\begin{cases}\left(\frac{1}{3}\right)^x+1,\quad x\in[-1,0],\\\log_2(x+1),\quad x\in(0,3).\end{cases}@i Určete obor hodnot funkce @if@i.
Jedná o příklad tzv. funkce definované po částech. Je třeba zaměřit se na každou část definičního oboru zvlášť a pro ni zakreslit danou funkci. Je vhodné si nakreslit větší část grafu a potom jen zvýraznit tu část grafu, která odpovídá zadanému rozpětí pro @ix@i. Z obrázku musí být zřetelné, o jaký graf se jedná.
Na intervalu @i[-1,0]@i je funkce @if@i definována jako posunutá exponenciála o základu @i \frac 13@i. Neboť základ je menší než jedna, jedná se o klesající funkci. Posunutí je o 1 nahoru. Na obrázku je tato část grafu funkce @if@i načrtnutá modrou barvou. Ta část exponenciály, která není součástí grafu @if@i, je vyznačena čárkovaně. Krajní body jsou součástí grafu @if@i, což je vyznačeno plnými kolečky na koncích modré části grafu. Na zbývající části definičního oboru je grafem @if@i logaritmická křivka posunutá o 1 doleva. V obrázku je načrtnutá červeně, včetně posunuté asymptoty, přebývající část opět čárkovaně. Tato část grafu @if@i je zakončena prázdnými kolečky, čímž naznačíme, že tyto body již nejsou součástí grafu funkce @if@i (@ix=3@i neleží v definičním oboru funkce @if@i a @if(0)@i je definováno podle první (modré) části grafu @if@i). U krajních bodů grafu je třeba ještě určit funkční hodnoty. Obor hodnot @iH(f)@i vyčteme z grafu @if@i jako jeho pravoúhlý průmět na osu @iy@i. Dostáváme @i\mathcal H(f)=(0,2) \cup [2,4]=(0,4]@i.
Užitečná poznámka: Jelikož nemáme nekonečný papír, črtáme vždy jen část grafu. Je třeba dát jasně najevo, co se s funkcí děje dál. Jsou tři možnosti, buďto je graf ukončen bodem (plný nebo prázdný bod, podle definičního oboru), nebo je naznačeno, že se přibližuje k nějaké asymptotě, nebo pokračuje do nekonečna.

Neřešené příklady
- Načrtněte graf funkce @if(x)=\begin{cases}\sqrt[3]{x+1},\quad x<0,\\ 0,\qquad x=0, \\\frac{1}{x}+1,\quad x\in(0,2].\end{cases}@i Určete obor hodnot.
- Načrtněte graf funkce @if(x)=\begin{cases}-\cos\frac{x}{2},\quad x<0,\\1+\ln(x+1),\quad x\ge 0.\end{cases}@i
- Načrtněte graf funkce @if(x)=\begin{cases}2+\sqrt{-x},\quad x\in[-4,0),\\1,\qquad x=0,\\1-\frac{1}{(x+1)^2},\quad x>0.\end{cases}@i



