Operace s funkcemi
Operace s funkcemi

Teoretické minimum
Základní operace, pomocí kterých z několika funkcí vzniká funkce nová, jsou součet, rozdíl, součin, podíl a skládání funkcí. Mějme dvě funkce @if@i a @ig@i s definičními obory @i\mathcal D(f),\mathcal D(g)@i.- Součet funkcí @if+g@i je definován jako @i(f+g)(x)=f(x)+g(x)@i, definiční obor @iD(f+g)=D(f)\cap D(g)@i.
- Rozdíl funkcí @if-g@i je definován jako @i(f-g)(x)=f(x)-g(x)@i, definiční obor @iD(f-g)=D(f)\cap D(g)@i.
- Součin funkcí @if\,g@i je definován jako @i(fg)(x)=f(x)g(x)@i, definiční obor @iD(fg)=D(f)\cap D(g)@i.
- Podíl funkcí @if\,/\,g@i je definován jako @i(f/g)(x)=f(x)/g(x)@i, definiční obor @iD(f/g)=D(f)\cap D(g)\setminus\left\lbrace x\in D(g)\, |\,g(x)=0\right\rbrace@i.
Všimněme si, že výsledná funkce je definovaná pro taková @ix@i, pro která jsou definované obě původní funkce (a při kterých nevzniká dělení nulou v případě podílu). Je-li například @if(x)=\log x@i s definičním oborem @i\mathcal D(f)=(0, \infty)@i a @ig(x)=\sqrt{2-x}@i s definičním oborem @i\mathcal D(g)=(- \infty, 2]@i, pak jejich součtem je funkce @i(f+g)(x)=\log x+\sqrt{2-x}@i s definičním oborem @i\mathcal D(f+g)=(0, 2]@i.
Poslední operace je složitější a zajímavější.
- Složení funkcí @if\circ g@i je definováno jako @i(f\circ g)(x)=f(g(x))@i.
Proměnná @i x@i je tedy zobrazena nejprve funkcí @ig@i (říkáme jí vnitřní funkce) a obdržený výsledek @ig(x)@i je následně zobrazen funkcí @i f@i (tzv. vnější funkcí) na hodnotu @if(g(x))@i. Tuto operaci lze provést pouze pro ta @i
x@i z definičního oboru funkce @ig@i, jejichž obraz @ig(x)@i padne do definičního oboru funkce @if@i. Tedy @i D(f\circ g)=\left\lbrace x\in D(g)\, | \, g(x) \in D(f)\right\rbrace@i.
Uvažujme například funkce @if(x)=\sqrt x@i a @ig(x)=x^3-1@i. Složená funkce @ih=f\circ g@i je pak @ih(x)=(f\circ g)(x)=f(g(x))=f(x^3-1)=\sqrt{x^3-1}@i. Definičí obor funkce @ig@i jsou sice všechna reálná čísla, my ale můžeme
uvažovat pouze ta @ix@i, pro jejichž obraz @ix^3-1@i je definovaná funkce odmocnina, tedy @ix\in[ 1,\infty)@i. Neboli @i D(h)=[ 1,\infty)@i.
Všimněme si, že u skládání funkcí záleží na jejich pořadí. Při složení funkcí @ig@i a @if@i v opačném pořadí dostáváme @ij(x)=(g\circ f)(x)=g(f(x))=g(\sqrt x)=(\sqrt x)^3-1@i s definičním oborem @iD(j)=[ 0,\infty)@i.
Můžeme složit i tři a více funkcí, například @if\circ g\circ\ h@i je definována jako @i(f\circ g\circ\ h)(x)=f(g(h(x)))@i. Obor hodnot složené funkce určujeme tak, že její definiční obor postupně zobrazíme jednotlivými funkcemi složení počínaje tou nejvíc vnitřní.
Související
Funkce, limita funkce, derivace funkce, integrace funkce.
Řešené příklady
1. Jsou dány funkce @if(x)=\ln{x}@i a @ig(x)=x+2@i. Napište předpis složených funkcí @if\circ g@i a @ig\circ f@i včetně jejich definičních oborů.
Předpis funkce @if\circ g@i získáme tak, že nejprve použijeme funkci @ix+2@i a poté logaritmus, tedy @i(f\circ g) (x)=f(g(x))=\ln(x+2)@i. Postupem posaným v první kapitole určíme definiční obor, @iD(f\circ g)=(-2,\infty)@i. Podobně postupujeme u funkce @ig\circ f@i, dostáváme @i(g\circ f)(x)=g(f(x))=\ln x + 2@i, definičním oborem @iD(g\circ f)=(0,\infty)@i.
Užitečná poznámka: Všimněme si, jak se v zápisu funkcí pracuje se závorkami. Je-li v argumentu funkce součet nebo rozdíl, musíme závorky psát, u součinu a podílu ne. Předpisy @i\ln(x+2)@i a @i\ln x +2@i nevyjadřují tutéž funkci! Můžeme ale psát například @i\ln 2x@i. Pokud by mělo dojít k nejednoznačnosti, použijeme raději závorky, nebo příslušný činitel napíšeme před funkci. Například místo nejednoznačného @i\sin x .y@i je lepší napsat @iy\sin x@i, anebo @i\sin (xy) @i.2. Jsou dány funkce @if(x)=\frac{1}{x},g(x)=1-x@i a @ih(x)=\sqrt{x}@i. Napište předpis složené funkc @ih\circ g\circ f@i a její definiční obor.
Nejvíc vnitřní funkce je @i\frac{1}{x}@i, tou začneme. Pokračuje odečítáním od jedničky @i1-x@i a nakonec odmocninou @i\sqrt x@i. Dostáváme tak funkci @i(h\circ g\circ f)(x)=h(g(f(x)))=\sqrt{1-\frac{1}{x}}@i. Pro určení definičního oboru řešíme nerovnici
@b1-\frac{1}{x}\ge 0.@b
Tuto nerovnici můžeme řešit například převedením na nerovnici v podílovém tvaru @b1-\frac{1}{x}=\frac{x-1}{x}\ge 0.@b
Výsledkem je @i\mathcal D(h\circ g\circ f)=(-\infty,0)\cup[1,\infty)@i.
3. Rozložte funkci @if(x)=\cos\sqrt{x^2-1}@i na elementární funkce.
Definiční obor zadané funkce je @i(-\infty,-1]\cup[1,\infty)@i. Můžeme ji rozložit například na 4 funkce, @if=f_1\circ f_2\circ f_3\circ f_4@i, kde @b\begin{array}{ll} f_1(x)&=\cos x,\\ f_2(x)&=\sqrt{x},\\ f_3(x)&=x-1,\\ f_4(x)&=x^2.\end{array}@b Všimněte si, že součástí odpovědi je nejen předpis jednotlivých funkcí, ale i pořadí, v jakém jsou složeny.
4. Najděte definiční obor a obor hodnot funkce @if(x)=\left( 1+\mathrm{e}^x\right)^2@i.
Definiční obor funkce je množina reálných čísel. Obor hodnot získáme pomocí rozkladu @if@i na elementární funkce. Platí @if=f_1\circ f_2\circ f_3,@i kde @b\begin{array}{ll} f_1(x)&=x^2,\\ f_2(x)&=1+x,\\ f_3(x)&=\mathrm{e}^x.\end{array}@b
Definiční obor funkce @if@i zobrazujeme postupně jenotlivými funkcemi z rozkladu počínaje tou nejvíc vnitřní. Při zobrazení jednotlivých intervalů využíváme znalost Tabulky I.
Funkce @if_3(x)=\mathrm{e}^x@i zobrazí množinu všech reálných čísel @i(-\infty,\infty)@i na množinu všech kladných čísel @i(0,\infty)@i. Nyní se obor hodnot @i\mathcal H(f_3)=(0,\infty)@i se stává definičním oborem následující funkce ve složení, tedy funkce @if_2@i. Funkce @if_2(x)=1+x@i (přičtení jedničky) zobrazí interval @i(0,\infty)@i na interval @i(1,\infty)@i. Funkce @if_1(x)=x^2@i pak zobrazí interval @i(1,\infty)@i opět na @i(1,\infty)@i, viz obrázek níže. Zapisujeme například takto:
@b\mathcal D(f)=(-\infty,\infty)\xrightarrow{\mathrm{e}^x} (0,\infty) \xrightarrow{x+1}(1,\infty)\xrightarrow{x^2}(1,\infty)=\mathcal H(f)@b
Tento a následující obrázky ilustrují, jak se zobrazují intervaly příslušnou elementární funkcí. Interval pro proměnnou @ix@i, vyznačený modře, se promítne svisle na graf funkce a posléze vodorovně na osu @iy@i, obraz je zobrazen červeně.

5. Najděte definiční obor a obor hodnot funkce @if(x)=\sqrt{1-\ln\sqrt{x}}@i.
Postupujeme stejně jako v předchozím příkladě. Definiční obor @i\mathcal D(f)=(0,\mathrm{e}^2]@i. Funkci @if@i rozložíme na elementární funkce @if=f_1\circ f_2\circ f_3\circ f_4@i, kde
@b\begin{array}{ll} f_1(x)&=\sqrt{x},\\ f_2(x)&=1-x,\\ f_3(x)&=\ln x,\\ f_4(x)&=\sqrt{x}.\end{array}@b Obor hodnot @i\mathcal H(f)@i získáme z postupným zobrazováním definičního oboru @i\mathcal D(f)@i jednotlivými funkcemi ze složení:
@b\mathcal D(f)=(0,\mathrm{e}^2]\xrightarrow{\sqrt{x}} (0,\mathrm{e}] \xrightarrow{\ln{x}}(-\infty,1]\xrightarrow{1-x}[0,\infty)\xrightarrow{\sqrt{x}}[0,\infty)=\mathcal H(f)@b
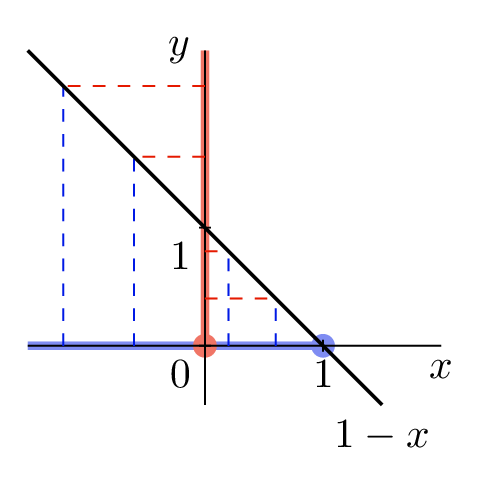
Na prvním obrázku ilustrujeme, že funkce @if_3(x)=\ln x@i zobrazí interval @i(0,\mathrm{e}]@i na interval@i(-\infty,1]@i. Tento interval je následně zobrazen funkcí @if_2(x)=1-x@i na interval @i(0,\infty)@i, viz druhý obrázek.

6. Najděte definiční obor a obor hodnot funkce @if(x)=\ln\frac{x+1}{x}@i.
Definiční obor je @i\mathcal D(f)=(-\infty,-1)\cup(0,\infty)@i. Rozklad na elementární funkce nelze provést přímo, vnitřní funkce obsahuje podíl. Zadanou funkci ale můžeme přepsat jako @if(x)=\ln\frac{x+1}{x}=\ln\left(1+\frac{1}{x}\right)@i.
Užitečná poznámka: Fakt, že se jedná o čistě složenou funkci, poznáme tak, že se v předpisu funkce @if@i objevuje symbol proměnné x pouze jednou.
Při určování oboru hodnot zobrazujeme celý definiční obor @i\mathcal D(f)@i, tedy oba intervaly.
@b\mathcal D(f)=(-\infty,-1)\cup(0,\infty)\xrightarrow{\frac{1}{x}} (-1,0)\cup(0,\infty) \xrightarrow{1+x}(0,1)\cup(1,\infty)\xrightarrow{\ln x}(-\infty,0)\cup(0,\infty)=\mathcal H(f)@b
Lomená funkce @i\frac{1}{x}@i zobrazí interval @i(0,\infty)@i opět na interval@i(0,\infty)@i. Interval @i(-\infty,-1)@i je funkcí @i\frac{1}{x}@i zobrazen na interval @i(0,-1)@i, viz následující obrázek.

Neřešené příklady
- Jsou dány funkce @if(x)=\sqrt{x}@i a @ig(x)=\log x@i. Napište předpis složených funkcí @if\circ g@i a @ig\circ f@i a určete jejich definiční obory.
- Jsou dány tři funkce, @if(x)=x^3,g(x)=x+1@i a @ih(x)=\sin x@i. Napište předpisy složených funkcí @if\circ g\circ h,h\circ g\circ f@i a @ig\circ f \circ h@i.
- Určete definiční obor funkce @if(x)=\sqrt{1-\ln^3(x+1)}@i, rozložte ji na elementární funkce a pomocí rozkladu nalezněte obor hodnot.
- Určete definiční obor funkce @if(x)=(\cos x+2)^2@i, rozložte ji na elementární funkce a pomocí rozkladu nalezněte obor hodnot.
- Určete definiční obor funkce @if(x)=\sin\sqrt{\ln(x)-1}@i, rozložte ji na elementární funkce a pomocí rozkladu nalezněte obor hodnot.
- Určete definiční obor funkce @if(x)=\ln\frac{1-x}{1+x}@i, rozložte ji na elementární funkce a pomocí rozkladu nalezněte obor hodnot.
