Zavedení pojmu funkce, lineární a kvadratická funkce, grafické řešení kvadratických nerovnic
Zavedení pojmu funkce, lineární a kvadratická funkce, grafické řešení kvadratických nerovnic

Teoretické minimum
Funkce je naprosto zásadní pojem nejen v matematice, proto byste mu měli dobře rozumět. Představte si fungující automat na láhve. Podle toho kolik vložíte do automatu láhví, obdržíte cedulku s částkou peněz. Funkce je takový "matematický stroj (automat)". Do funkce vložíte nějaký vstup (láhve) a funkce vrátí nějaký výstup (suma peněz). Úkolem funkce tedy je převzít nějaké číslo (vstup), něco s ním provést, změnit ho a následně toto nové číslo vrátit (výstup).
Funkce popisuje závislost jedné veličiny na druhé. V případě automatu na láhve tuto závislost vystihuje následující tabulka, kde v prvním sloupečku je počet láhví a ve druhém je hotovost, která nám bude vrácena.
@b \begin{array}{|c|c||} \hline \textrm{počet láhví}&\textrm{částka v Kč} \\ \hline 1&3\\ \hline 2&6\\ \hline3&9\\ \hline 4&12\\ \hline 5&15\\ \hline \end{array} @b
Každá funkce má jméno. V matematice je zvykem označovat funkce malými písmenky @i\, f,g, h, \ldots\,@i. Označíme-li automat na láhve písmenkem @i\,f@i, pak první řádek tabulky zapíše takto: @b f(1)=3.@b Funkce @i\,f\,@i přiřadí @i1@i (láhev) právě jednu hodnotu @i3@i (částka). Funkcí rozumíme předpis @i\,f@i, který každému prvku @i\,x\,@i z jisté množiny @i\,M\,@i přiřadí právě jeden prvek @i\,y\,@i z jisté množiny @i\,N@i. Píšeme @by=f(x).@b Právě jeden prvek @i\,y\,@i znamená, že nemůže nastat, že by funkce pro stejný vstup mohla vrátit dva různé výstupy, že bychom za jednu a tutéž láhev mohli dostat různou sumu peněz. Naše množiny @i\,M, N\,@i budou podmnožiny množiny reálných čísel @i\mathbb{R}@i. Mluvíme pak přesněji o reálné funkci (hodnoty proměnné @i\,y\,@i jsou reálná čísla) jedné reálné proměnné (hodnoty proměnné @i\,x\,@i jsou reálná čísla). Nejčastěji budeme používat zkrácené pojmenování funkce @i\,f\,@i proměnné @i\,x@i. Proměnnou @i\,x\,@i nazýváme nezávisle proměnnou a proměnnou @i\,y\,@i závisle proměnnou (funkční hodnotou). Množinu @i\,M\,@i (množinu všech reálných čísel @i\,x@i, pro která má výraz @i\,f(x)\,@i smysl) nazýváme definiční oborem funkce @i\,f\,@i a značíme @i \mathcal D(f)@i. Množinu těch čísel @i\,y\in N\,@i (množinu funkčních hodnot @i\,f(x)@i), na které se zobrazuje nějaké číslo @i\,x\in \mathcal D(f)@i, nazýváme oborem hodnot funkce @i\,f\,@i a značíme @i \mathcal H(f)@i. Grafem funkce rozumíme množinu uspořádaných dvojic nezávisle proměnné a příslušné funkční hodnoty, tj.
@b {\rm graf} f=\{(x,y); x\in\mathcal D(f), y=f(x) \}.@b
Vraťme se k automatu na láhve. V tabulce platí, že výstup je trojnásobkem vstupu. Pomocí funkčního předpisu to zapíšeme takto : @b f(x)=3\cdot x.@b Co nám předpis říká? Písmeno @i\,f\,@i je název funkce. Proměnná @i\,x\,@i (argument funkce) je v závorkách, je nezávislá a schovává se za ní počet láhví, které do automatu hodíme. Vložíme-li do automatu @i\,4\,@i láhve, je @i\,x=4\,@i a dál si automat (funkce) s touto hodnotou pracují po svém. Funkce se řídí předpisem, který je za rovnítkem. Po vynásobení proměnné @i\,x\,@i trojkou obdržíme funkční hodnotu (závisle proměnnou) @i\,y=3\cdot x@i. Lísteček s částkou peněz, které nám budou vráceny (@i f(4)=3\cdot 4=12\,@i Kč). Je to příklad lineární funkce.
Lineární funkce je každá funkce daná předpisem @b f(x)=ax+b,\quad a\neq 0.@b Výraz @i\,ax+b\,@i má vždy smysl, definičním oborem jsou všechna reálná čísla, tj. @i\,\mathcal D(f)=\mathbb R@i. Grafem je přímka o rovnici @i\,y=ax+b@i. Nakresleme graf funkce @i\,f(x)=3x@i. Přímka je jednoznačně daná dvěma body. Spočtěme dvě funkční hodnoty, např. @i\,f(1)=3, f(2)=6\,@i a zakreslíme v rovině s kartézskými souřadnicemi body o souřadnicích @i\,(1,3), (2,6)@i. Body vedeme přímku, viz následující obrázek
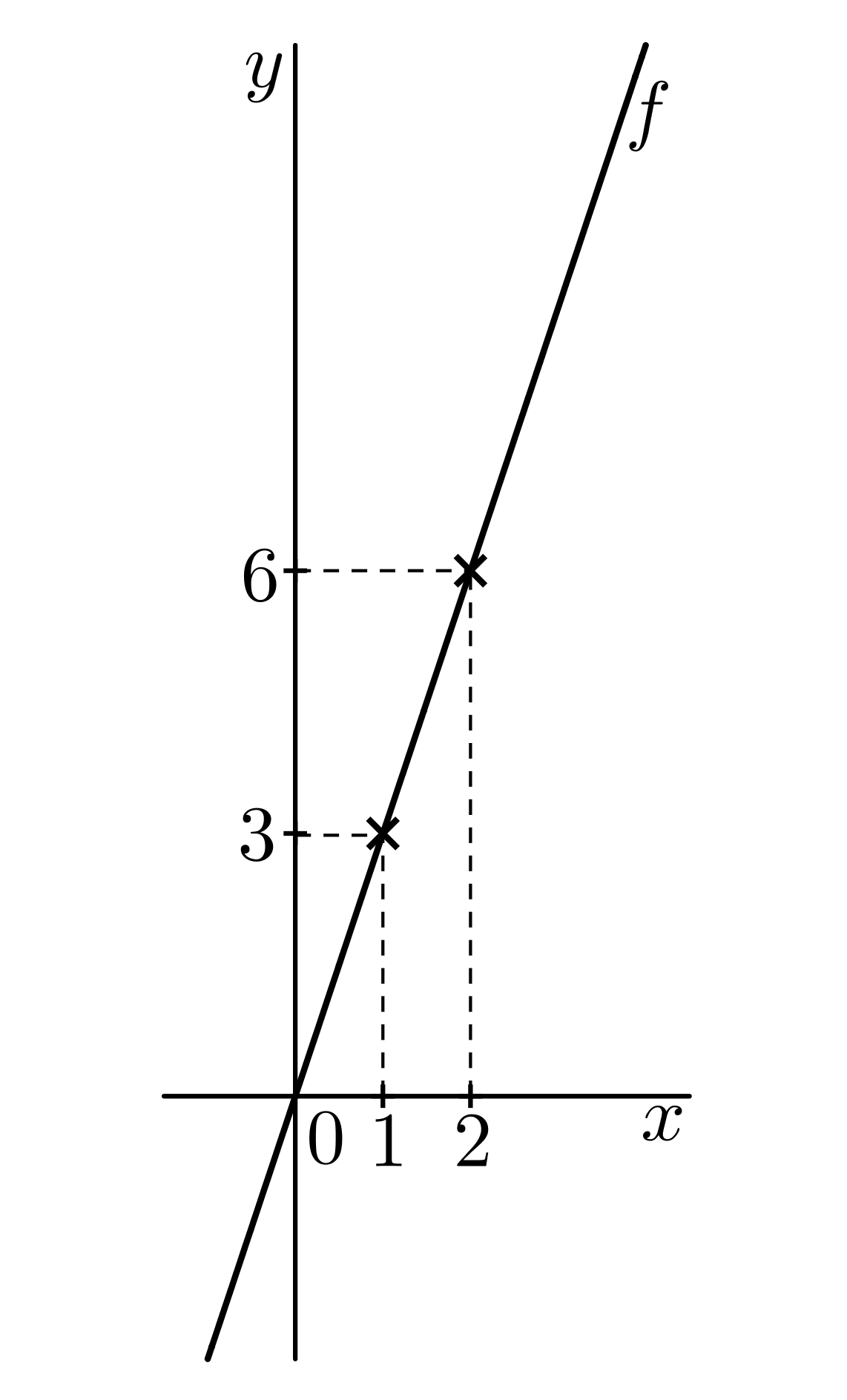
Z grafu snadno vyčteme obor hodnot. Funkční hodnoty leží na svislé ose @i\,y@i. Udělejme kolmý průmět přímky na osu @i\,y\,@i a máme obor hodnot, celou osu @i\,y@i, tj. @i\,\mathcal H(f)=\mathbb R@i.
Užitečná poznámka: Pokud je v předpisu lineární funkce @i\,b=0@i, tj. @i\,f(x)=ax,\ a\neq0@i, je grafem funkce @i\,f\,@i přímka procházející počátkem soustavy souřadné.
Užitečná poznámka: Pokud je @i\,a=0@i, tj. @i\,f(x)=b@i, mluvíme o konstantní funkci. Každému reálnému číslu @i\,x\,@i přiřadí funkce @i\,f\,@i stejnou funkční hodnotu @i\,b@i. Obor hodnot je jednoprvková množina @i\,\mathcal H(f)=\{b\}@i. Grafem je přímka rovnoběžná s osou @i\,x@i.
Kvadratická funkce je každá funkce daná předpisem @b f(x)=ax^2+bx+c,\quad a\neq 0.@b Výraz @i\,ax^2+bx+c\,@i má vždy smysl, definičním oborem jsou všechna reálná čísla, tj. @i\,\mathcal D(f)=\mathbb R@i. Grafem je parabola o rovnici @i\,y=ax^2+bx+c@i. Nakresleme graf funkce @b f(x)=2x^2+3x-2. @b Pokud je @i\,a>0@i, je parabola otevřená nahoru (funkce @i\,f\,@i je konvexní). Najdeme průsečíky grafu funkce @i\,f\,@i s
osu @i\,x@i, tj. dvojice @i\,(x,0)@i. Musíme vyřešit kvadratickou rovnici @i\,2x^2+3x-2=0@i. Diskriminat je @i\,D=9+16=25@i, tedy @b\,x_1=\dfrac{-3-5}{4}=-2,\qquad x_2=\dfrac {-3+5}{4}=\dfrac 12.@b Dále najdeme průsečík s osou @i\,y@i, tj. dvojici @i\,(0,f(0)\,)@i. Spočteme funkční hodnotu v nule: @i\,f(0)=-2@i. Zakreslíme
v rovině s kartézskými souřadnicemi body o souřadnicích @i\,(-2,0), (\frac 12,0), (0,-2)@i. Body vedeme parabolu, viz následující obrázek:
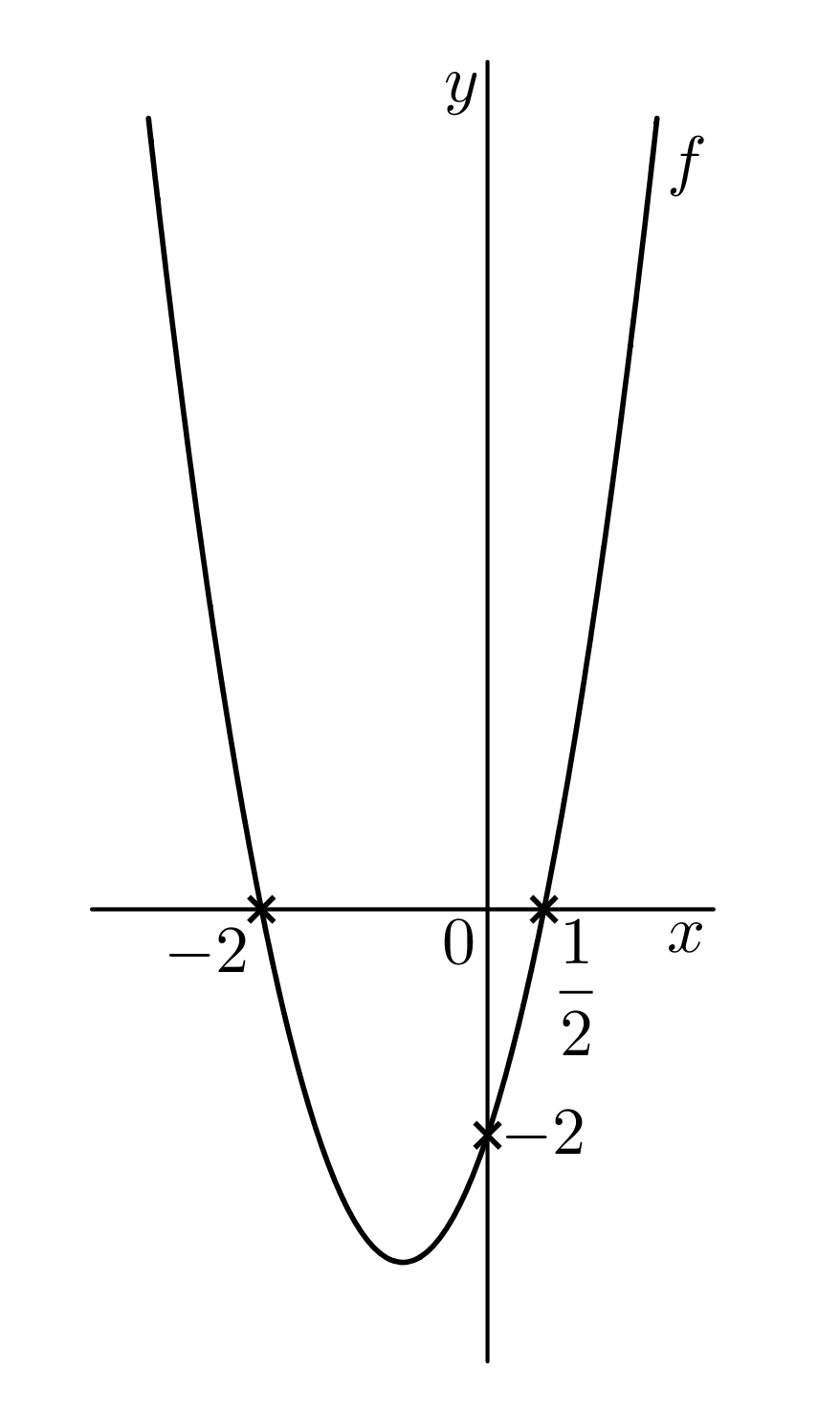
Z grafu vyčteme obor hodnot, pokud známe souřadnice vrcholu paraboly. Funkční předpis, mnohočlen, musíme doplnit na čtverec. @b f(x)=2x^2+3x-2=2\left(x^2+\dfrac 32\, x\right)-2=2\left(x^2+2\cdot x\cdot \frac 34+\dfrac 9{16}-\dfrac 9{16}\right)-2=2\left(x+\dfrac 34\right)^2-\dfrac 98-2=2\left(x+\dfrac 34\right)^2-\dfrac {25}8@b Souřadnice vrcholu paraboly jsou @i\,\left(-\,\dfrac 34,-\,\dfrac{25}8\right)@i. Obor hodnot je @i\,\mathcal H(f)=\left\langle -\,\dfrac{25}8, \infty\right)@i.
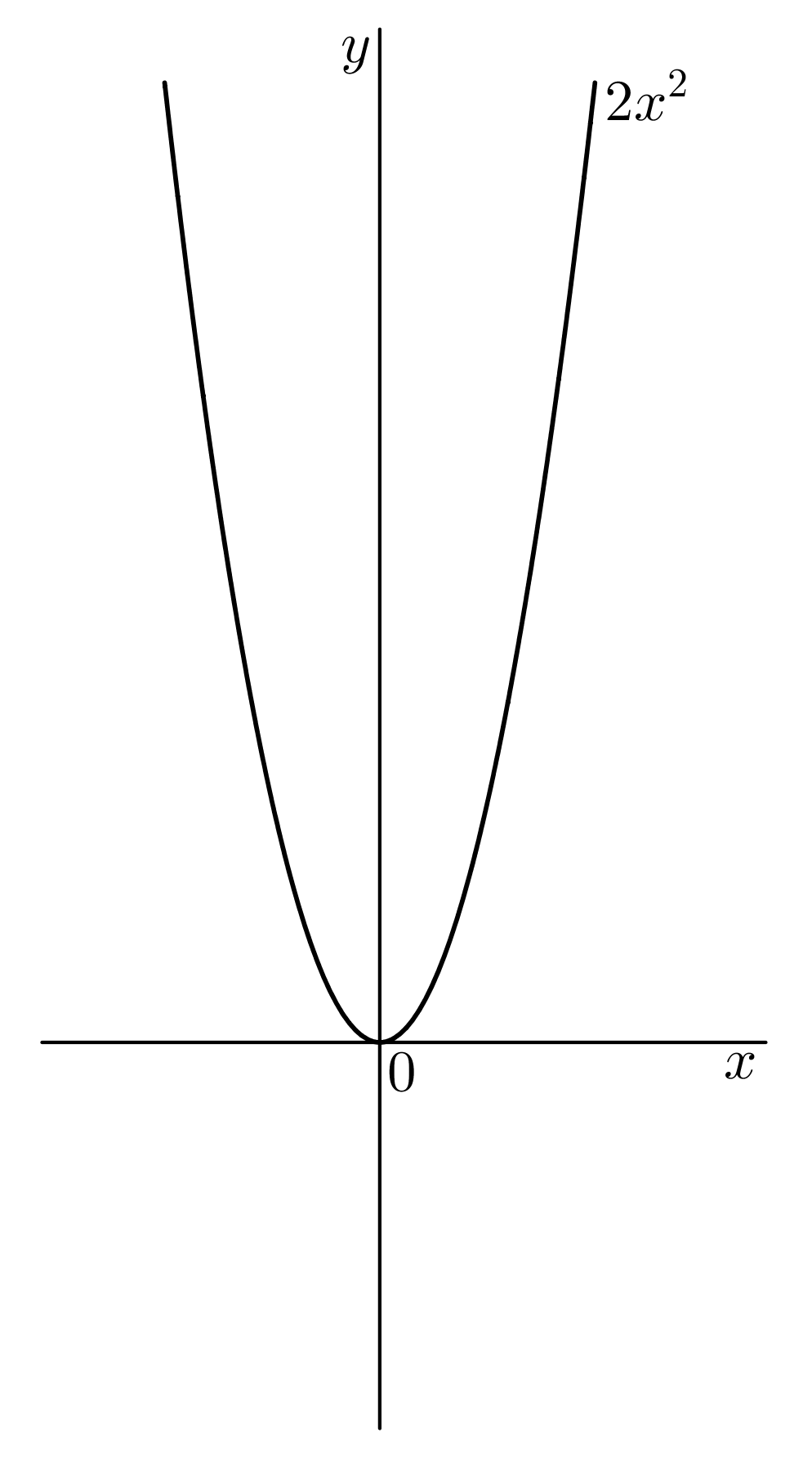
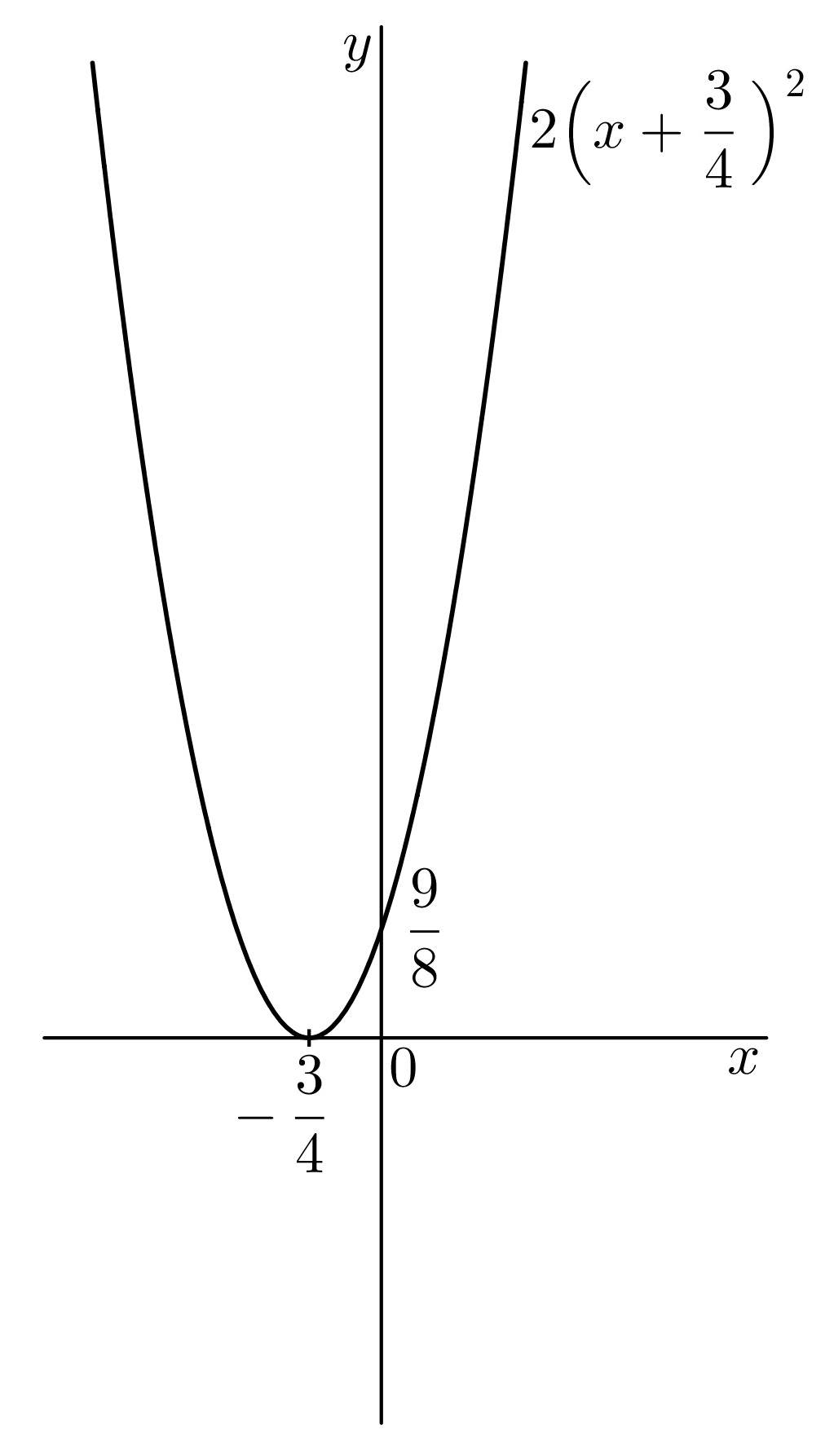
Užitečná poznámka: Graf funkce @i\,f(x)=2x^2+3x-2=2\left(x+\dfrac 34\right)^2-\dfrac {25}8@i, pokud jsme v předpisu udělali doplnění na čtverec, lze nakreslit na základě transformací souřadnic grafu funkce @i\,f(x)=x^2@i, viz kapitolka Graf funkce.
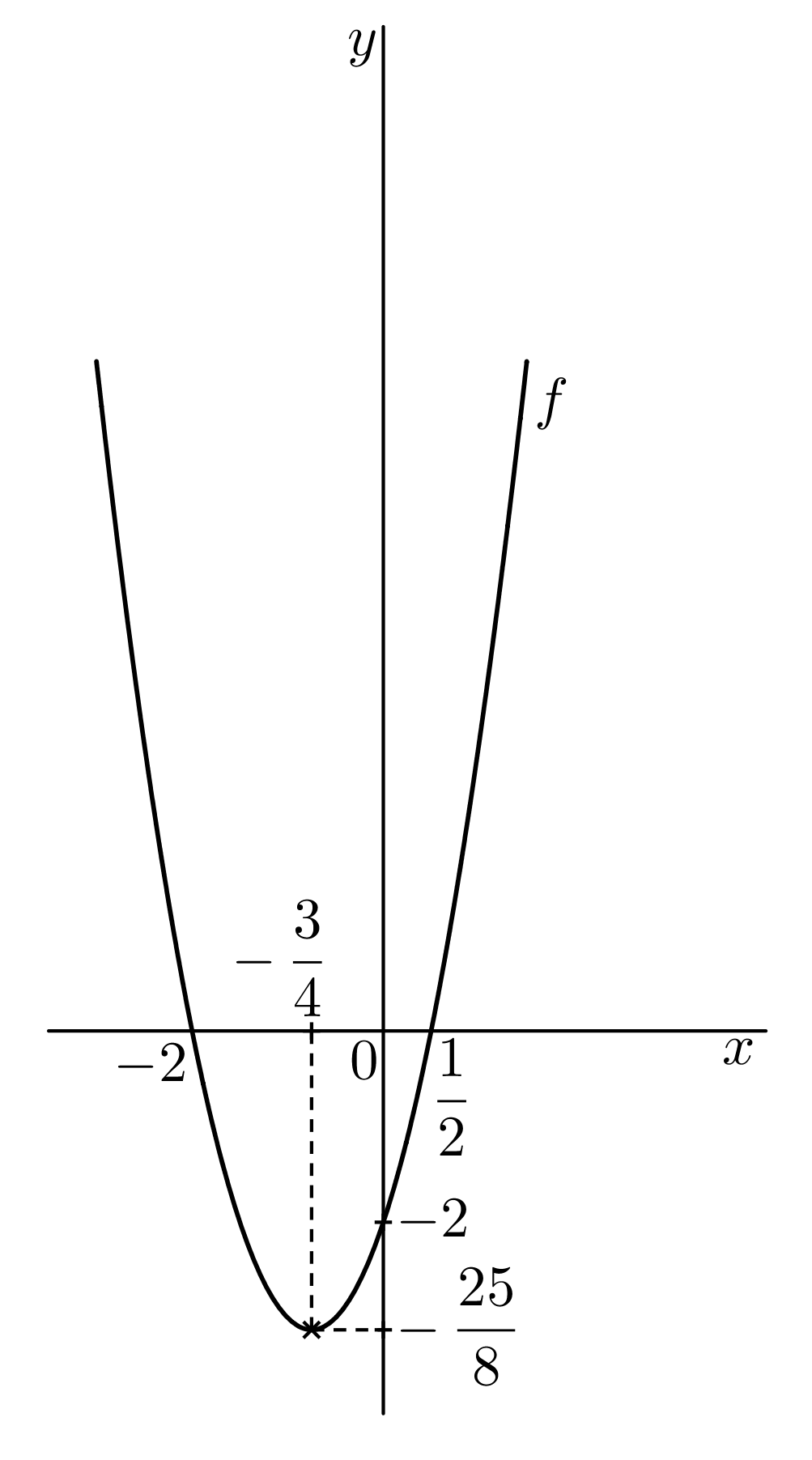
Užitečná poznámka: Vrchol paraboly leží na ose paraboly. Místo doplnění funkčního předpisu na čtverec lze udělat aritmetický průměr kořenů kvadratické rovnice @i\,2x^2+3x-2=0@i, pokud ovšem existují dva reálné kořeny, a tak získáme @i\,x@i-ovou souřadnici vrcholu, tj. @b \dfrac{-2+\frac{1}{2}}{2}=\dfrac{-\,\frac{3}{2}}{2}=-\,\dfrac 34.@b @i\,y@i-ová souřadnice vrcholu získáme vypočtením funkční hodnoty v bodě @i\,x=-\,\frac 34@i,@b f(-\,\frac{3}{4})=2\cdot\dfrac 9{16}+3\cdot \left(-\,\dfrac 34\right)-2=\dfrac 98-\dfrac 94-2=\dfrac{9-18-16}8=-\,\dfrac{25}8.@b
Užitečná poznámka: Grafem funkce @i\,f(x)=ax^2+bx+c@i, kde @i\,a<0@i, je parabola otevřená dolu. Funkce @i\,f\,@i je konkávní.
Související
Mnohočleny, lineární a kvadratická rovnice a nerovnice, definiční obor funkce, graf funkce.
Řešené příklady
- Určete definiční obor funkce @i\, f(x)=\dfrac {\sqrt{1-x}}{x^2+4}@i.
- Určete definiční obor funkce @i\, f(x)=\dfrac {x}{\sqrt{4x^2+20x+25}}@i.
- Řešte nerovnici @i\, x^2+4x-4<2x-x^2\, @i s reálnou neznámou @i\,x@i.
- Řešte nerovnici @i\, x^2+3\leq x+1\, @i s reálnou neznámou @i\,x@i.
Vypíšeme podmínky, za kterých má funkční předpis smysl. Druhá odmocnina je definovaná pro nezáporná čísla, tj. @i\ 1-x\geq 0\,@i a zároveň nelze dělit nulou, tj. @i\, x^2+4\neq 0@i. Z první nerovnosti plyne, že @i\,x\leq 1@i. Druhá podmínka je splněna vždy, @i\,x^2\neq -4\,@i pro všechna reálná čísla. Definiční obor je @i\,\mathcal D(f)=(-\infty, 1\rangle@i.
Užitečná poznámka: Nakreslete graf funkce @i\,g(x)=x^2+4@i, tj. parabolu @i\,y=x^2\,@i posunete ve směru osy @i\,y\,@i o dvě jednotky nahoru. Z obrázku vyčtete, že dokonce @i\,x^2+4\geq 4>0\,@i pro všechna reálná čísla.
Vypíšeme podmínky, za kterých má funkční předpis smysl. Druhá odmocnina je definovaná pro nezáporná čísla, tj. @i\ 4x^2+20x+25\geq 0\,@i a zároveň nelze dělit nulou, tj. @i\,\sqrt{4x^2+20x+25}\neq 0@i. Druhá odmocnina nabývá hodnoty nula jen pro nulu, proto @i\ 4x^2+20x+25\neq 0@i. Tedy musí platit
@b \begin{array}{r c l} 4x^2+20x+25&>& 0, \\[2mm] (2x+5)^2&>& 0, \\[2mm] 2x+5&\neq&0, \\[2mm] x&\neq& -\,\dfrac 52.\end{array}@b
Definiční obor je @i\,\mathcal D(f)=\mathbb R\backslash \left\{-\,\frac 52\right\}@i.
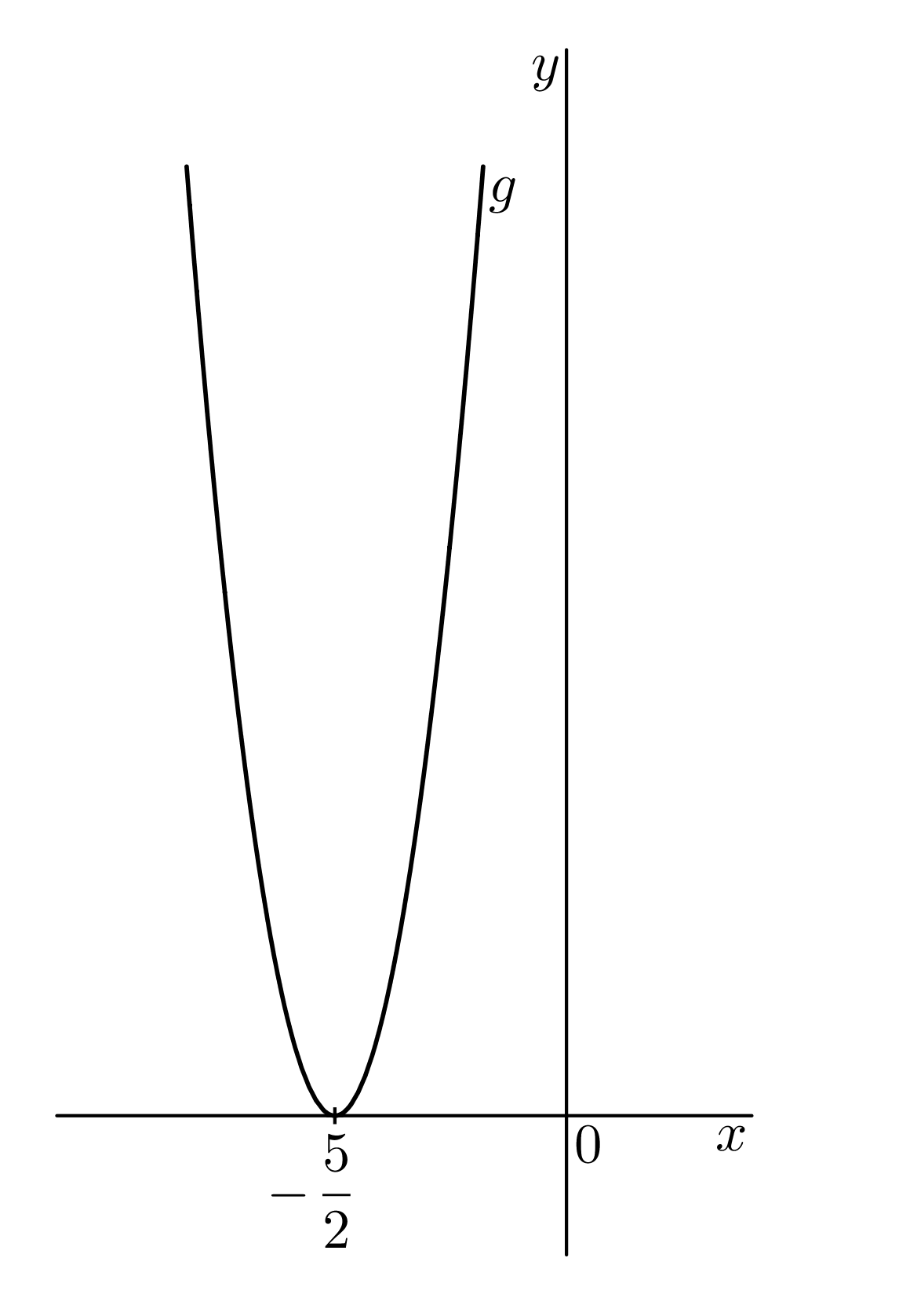
Užitečná poznámka: Při řešení nerovnice jsme použili vzorec @i\,A^2+2AB+B^2=(A+B)^2@i. K tomu je třeba trénig, zkušenosti. Kvadratickou nerovnici můžeme řešit graficky. Funkce @i\,g(x)=4x^2+20x+25\,@i je konvexní, graf (parabola) je otevřená nahoru. Rovnice @i\,4x^2+20x+25=0\,@i má jeden kořen, neboť @i\,D=400-400=0@i. Parabola má jeden průsečík s osou @i\,x@i, je to vrchol paraboly. Jeho @i\,x@i-ová
souřadnice je @i\,x=\dfrac{-20}8=-\,\dfrac 52@i. Řešením nerovnice jsou všechna @i\,x@i, pro která parabola leží nad osou @i\,x@i.
Nerovnici upravíme pomocí ekvivalentních úprav do anulovaného tvaru, tj. na pravé straně bude nula.
@b \begin{array}{r c l} x^2+4x-4&<& 2x-x^2\,/\ -2x+x^2 \\[2mm] 2x^2+2x-4&<& 0\,/\ :2 \\[2mm] x^2+x-2&<&0 \end{array}@b
Kvadratickou nerovnici můžete řešit algebraicky, viz kvadratické nerovnice nebo graficky. Stejné je, že nejprve najdeme kořeny rovnice @b x^2+x-2=0.@b Diskriminant je @i\,D=1+8=9@i. Rovnice má dva reálné kořeny @b x_1=\dfrac {-1-3}2=-2,\qquad x_2=\dfrac {-1+3}2=1.@b Graf funkce @i\,g(x)=x^2+x-2\,@i má dva průsečíky s osou @i\,x@i @b P_1=(-2,0),\quad P_2=(1,0).@b Funkce @i\,g(x)=x^2+x-2\,@i je konvexní (@i\,a=1>0\,@i), parabola @i\,y=x^2+x-2\,@i je otevřená nahoru, viz obrázek:
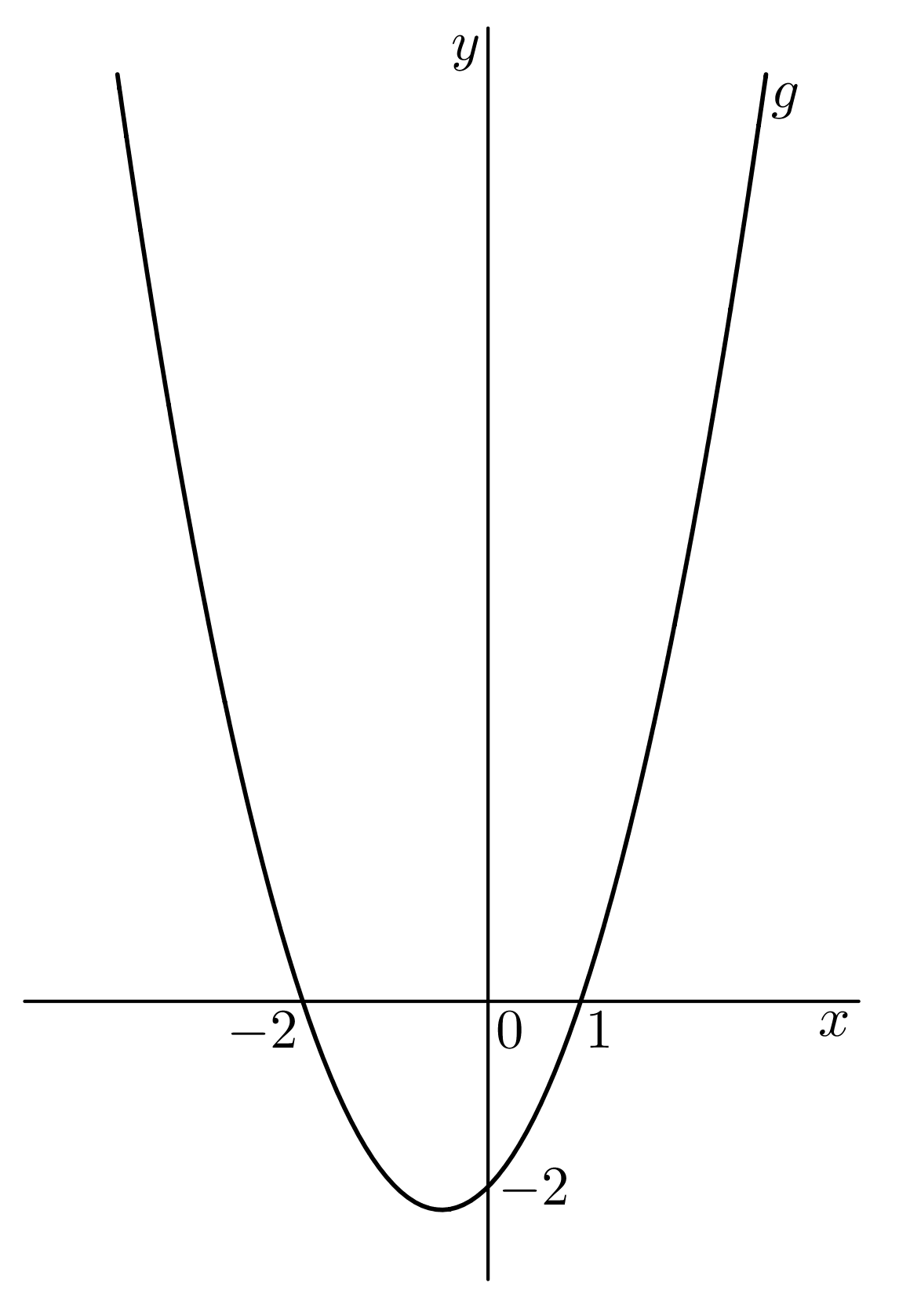
Hledáme ta @i\,x@i, pro která leží graf funkce @i\,g\,@i pod osou @i\,x@i. Platí, že pro @i\,x\in(-2,1)\,@i je @i\,g(x)<0@i. Nerovnice @b x^2+x-2<0@b má řešení @i\,K=(-2,1)@i.
Nerovnici upravíme pomocí ekvivalentních úprav do anulovaného tvaru.
@b \begin{array}{r c l} x^2+3&\leq& x+1\,/\ -x-1 \\[2mm] x^2-x+2&\leq& 0 \end{array}@b
Kvadratickou nerovnici budeme řešit graficky. Najdeme kořeny rovnice @b x^2-x+2=0.@b Diskriminant je @i\,D=1-8=-7<0@i. Rovnice nemá kořen. Graf funkce @i\,g(x)=x^2-x+2\,@i neprotne osu @i\,x@i. Funkce @i\,g(x)=x^2-x+2\,@i je konvexní (@i\,a=1>0\,@i), parabola @i\,y=x^2-x+2\,@i je otevřená nahoru, viz obrázek:
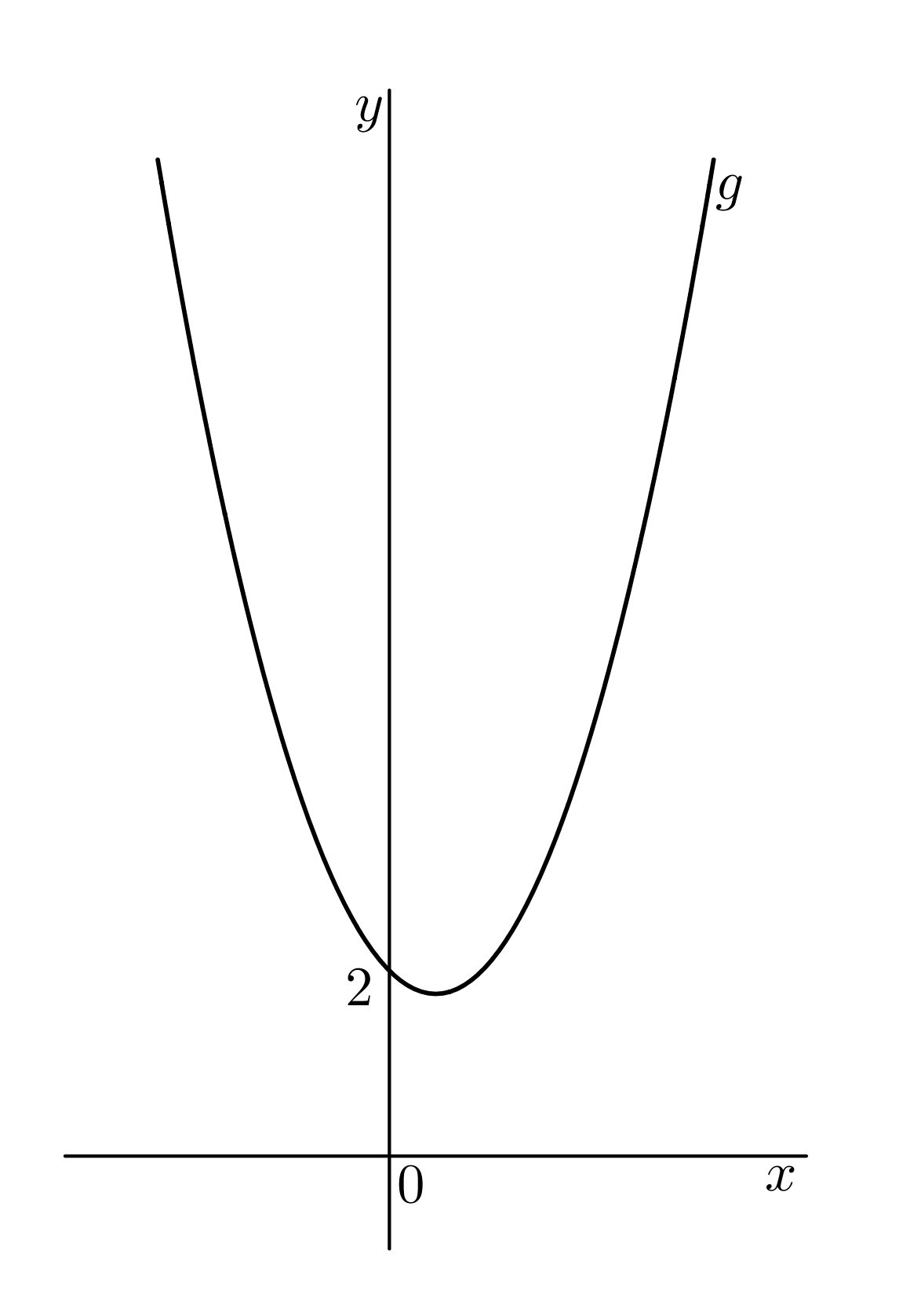
Platí, že pro všechna @i\,x\,@i je @i\,g(x)\geq 0@i. Nerovnice @b x^2-x+2\leq 0@b nemá řešení, tj. @i\,K=\emptyset@i.
Užitečná poznámka: Označme funkci na levé straně rovnice písmenkem @i\,f@i, tj. @i\,f(x)=x^2+3\,@i a funkci na pravé straně rovnice písmenkem @i\,g@i, tj. @i\,g(x)=x+1.@i Grafy funkcí zakresleme do jednoho obrázku:
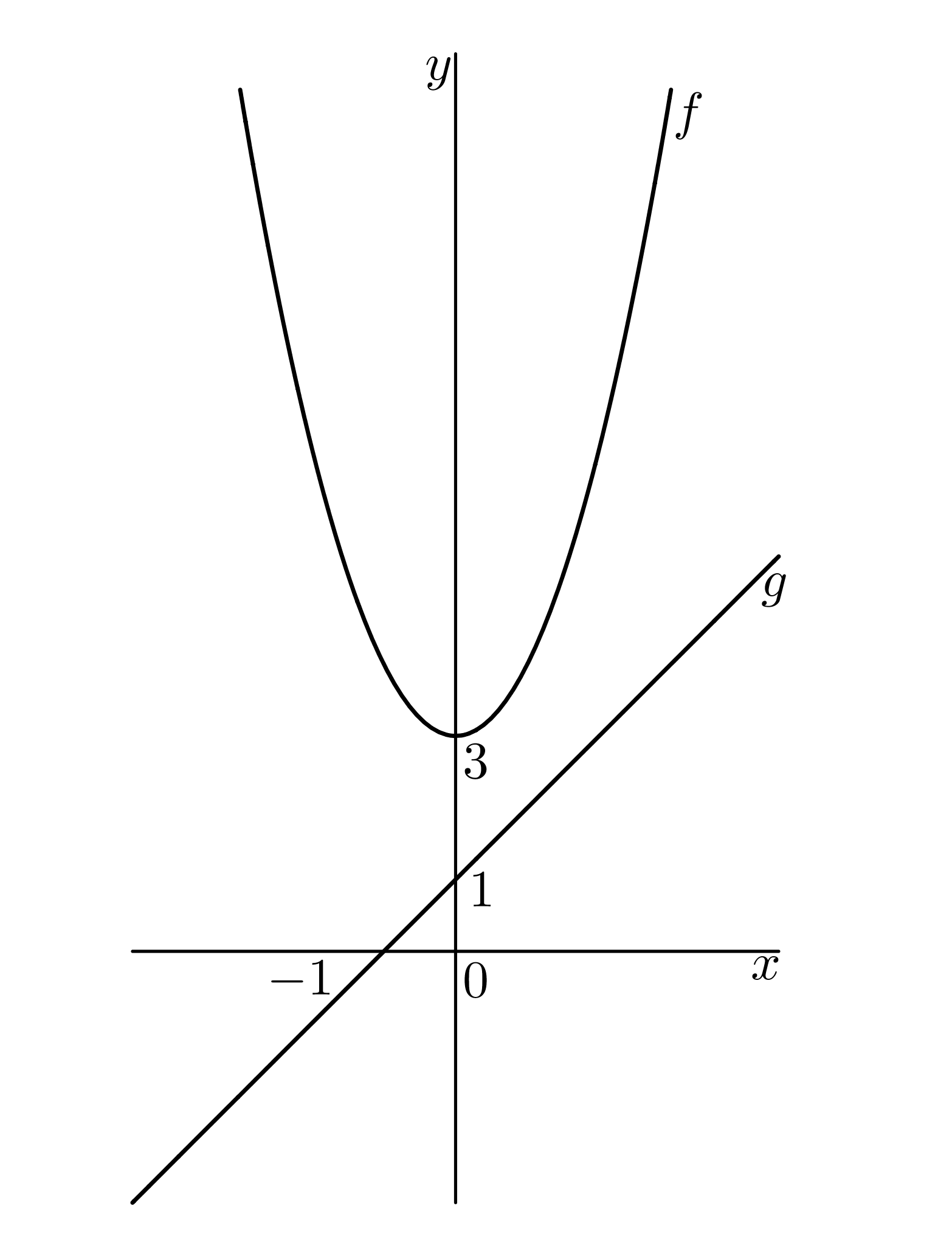
Hledáme ta @i\,x@i, pro která je funkční hodnota funkce @i\,f\,@i menší nebo rovna funkční hodnotě funkce @i\,g@i. Ovšem graf funkce @i\,f\,@i leží nad grafem funkce @i\,g@i, tedy pro všechna @i\,x\,@i platí, @i\,f(x)>g(x)@i. Nerovnice @i\,x^2+3\leq x+1\,@i nemá řešení.
Neřešené příklady
- Graficky řešte nerovnici @i 2(x+1)^2>(x-1)(x+2) @i.
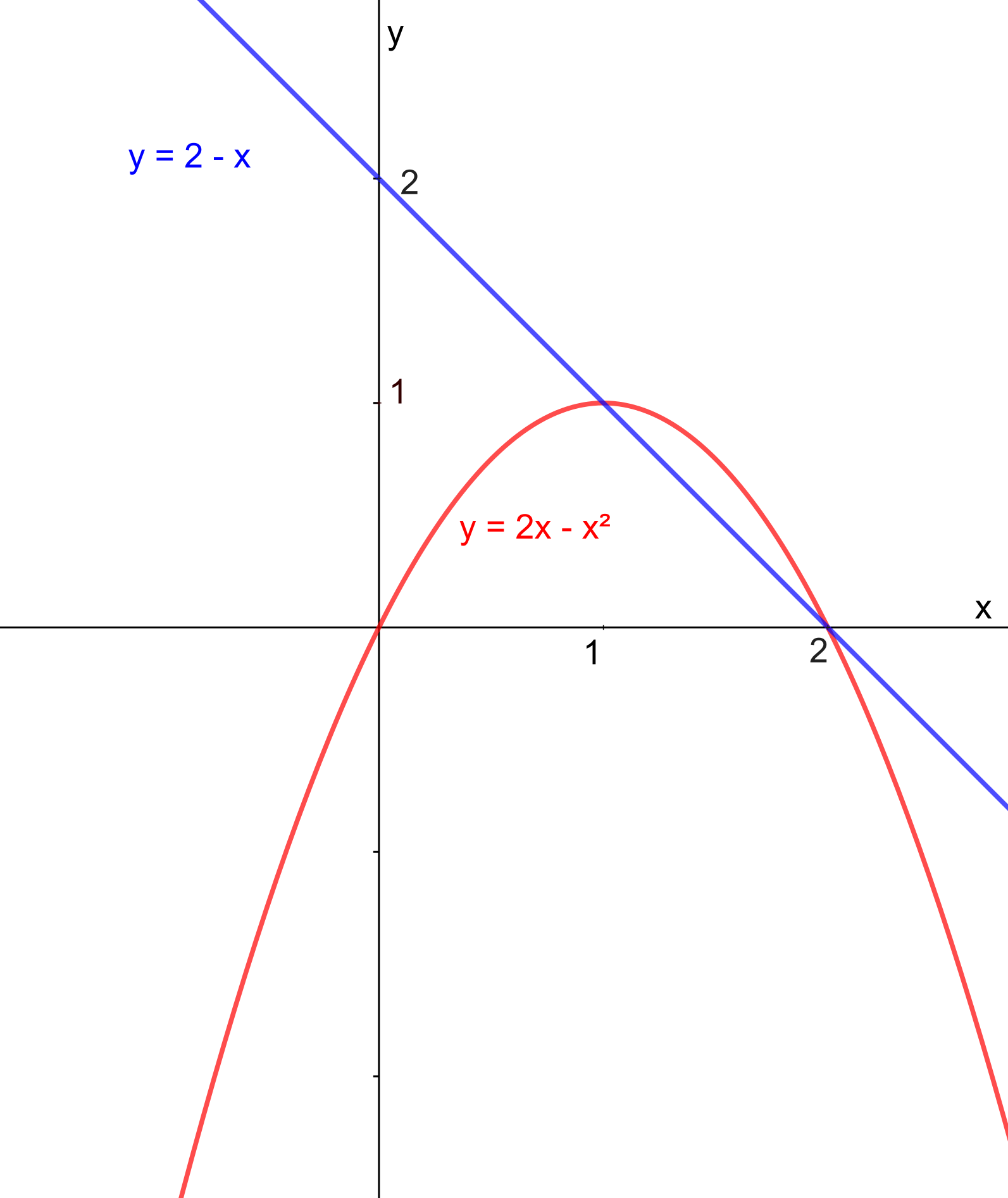
- Graficky řešte nerovnici @i 2x-x^2\geq 2-x@i.
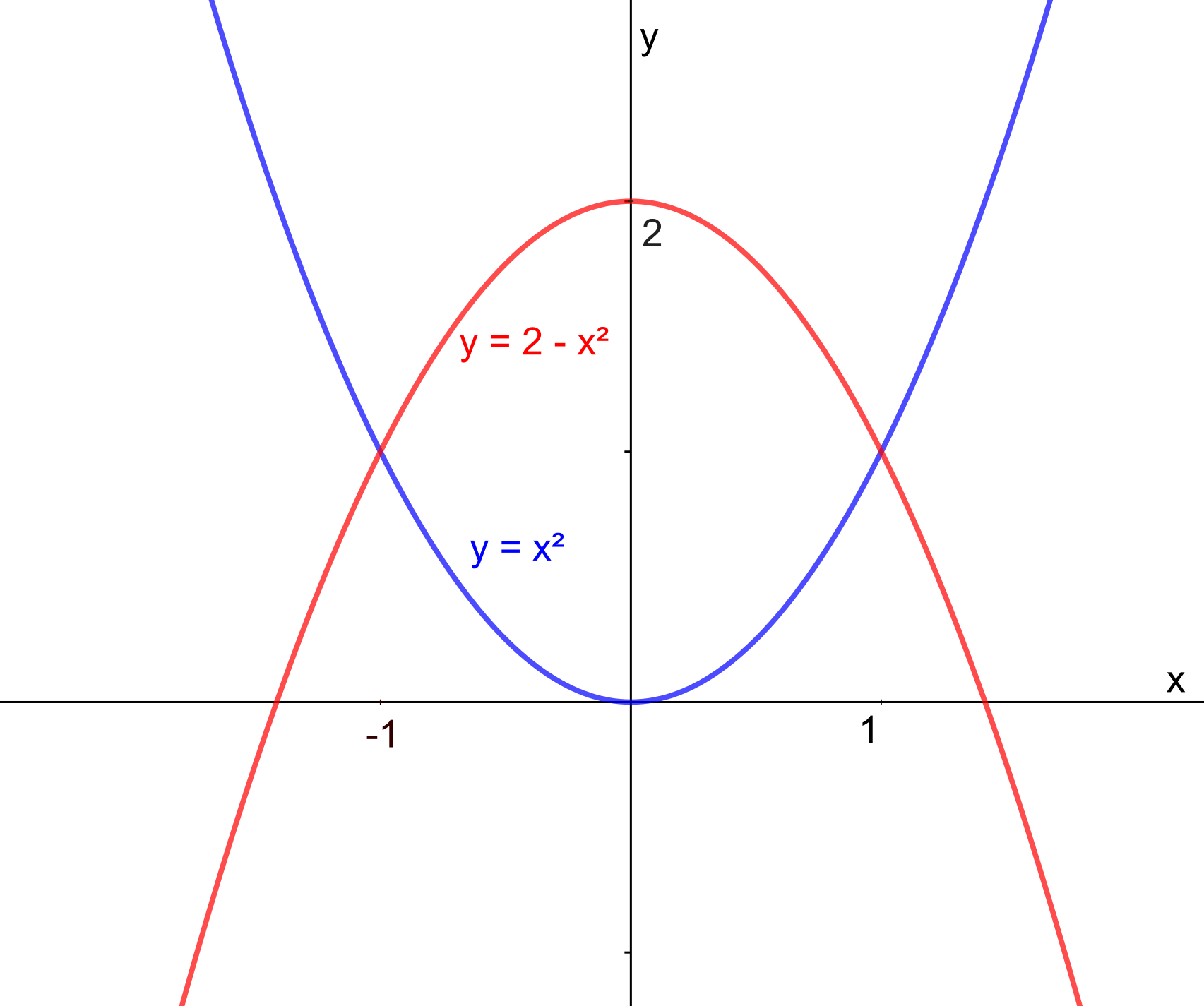
- Graficky řešte rovnici @i x^2=2-x^2.@i