Kvadratické nerovnice
Kvadratické nerovnice

Teoretické minimum
Kvadratickou nerovnicí s neznámou @i\ x@i rozumíme nerovnici, kterou lze ekvivalentními úpravami převést na tvar @b ax^2+bx+c>0,\qquad a,b,c\in\mathbb{R}, a\neq 0,@b resp. se znaménkem @i"\geq", "<", "\leq"@i.
Předpokládejme, že @i\,a>0@i. Pokud tomu tak není, vynásobíme obě strany nerovnice @i\, -1@i. Pozor, "nerovnítko" se obrátí. Nejprve najdeme kořeny kvadratické rovnice @b ax^2+bx+c=0.@b Pak kvadratický mnohočlen na levé straně nerovnice převedeme na součin kořenových činitelů, pokud to lze.
O počtu kořenů kvadratické rovnice @i\, ax^2+bx+c=0\,@i v oboru reálných čísel rozhoduje diskriminant @i D=b^2-4ac@i. Kvadratická rovnice má:
- pro @i\ D>0\ @i dva různé reálné kořeny @i\ x_{1}=\dfrac{-b+\sqrt D}{2a}@i, @i\ x_{2}=\dfrac{-b-\sqrt D}{2a}.@i Kvadratickou nerovnici přepíšeme na součinový tvar @b a(x-x_1)(x-x_2)>0@b a vyřešíme pomocí nulových bodů.
- pro @i\ D=0\ @i jeden reálný kořen (dvojnásobný kořen) @i\ x_{1,2}=-\,\dfrac{b}{2a}.@i Kvadratickou nerovnici přepíšeme na tvar @b a(x-x_1)^2>0@b což je za předpokladu @i\,a>0\,@i splněno pro všechna reálná @i\,x\neq x_1@i.
- pro @i\ D<0\ @i nemá reálné kořeny. Za předpokladu @i\,a>0\,@i platí, @b ax^2+bx+c>0@b pro všechna reálná@i\,x@i.
@b\begin{array}{rcl}-4(3-x)^2&\geq&11x-33/ -11x+33 \\[2mm] -4(9-6x+x^2)-11x+33&\geq&0\\[2mm]-4x^2+13x-3&\geq&0/ \cdot(-1)\\[2mm]4x^2-13x+3&\leq&0.\end{array}@b
Nejprve musíme najít kořeny rovnice @b 4x^2-13x+3=0.@b Pro rovnici platí @i\ a=4,\ b=-13,\ c=3@i. Vypočteme diskriminant: @i\ D=(-13)^2-4\cdot 4\cdot 3=169-48=121=(11)^2@i. Rovnice má dva reálné kořeny @bx_1=\dfrac{13+11}{8}=3,\qquad x_2=\dfrac{13-11}{8}=\dfrac 14.@b Nerovnici převedeme do součinového tvaru, tj. @b 4\Bigl(x-3\Bigr)\Bigl(x-\dfrac 14\Bigr)\leq 0@b Její nulové body jsou @i\, 3\,@i a @i\, \dfrac 14@i, které reálnou osu rozdělí na tři intervaly, pro které platí
@b \begin{array}{|c|c|c|c|c|c|c|} \hline \mathbb{R}&& \Bigl(-\infty,\dfrac14\Bigr)&\dfrac 14& \Bigl(\dfrac 14,3\Bigr)&3&\Bigl(3,\infty\Bigr)\\ \hline x-3 && -&- &- &0 & + \\ \hline x-\dfrac 14 &&
-&0&+ & + & +\\ \hline\\ \hline 4(x-3)\Bigl(x- \dfrac 14\Bigr) && \boldsymbol{+}& \bf{0}&{\bf -} &{\bf 0} & {\bf +}\\ \hline \end{array} @b
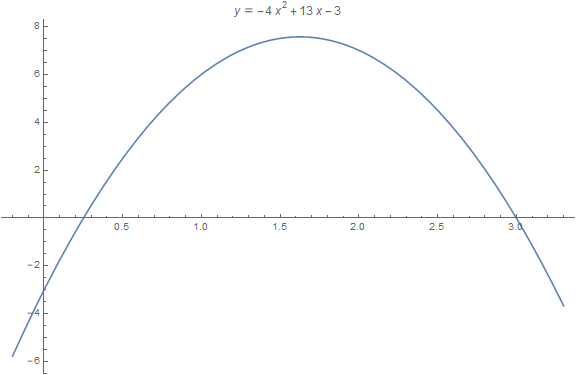
Užitečná poznámka: Uvědomme si, že počet reálných kořenů rovnice @i\ ax^2+bx+c=0,\ a\neq 0@i je roven počtu průsečíků paraboly @i\ y=ax^2+bx+c\ @i s osou @i\ x@i. Pokud je @i\,a<0\,@i je parabola "konkávní". Tedy celý postup řešení nerovnice @i\, -4x^2+13x-3\geq 0\,@i nahradí následující obrázek.
Související
Kvadratická rovnice, kvadratická funkce.
Řešené příklady
- Řešte nerovnici @i\, -5(1-x)^2<3x+11\,@i s reálnou neznámou @i\,x.@i
- Řešte nerovnici @ix^2-7\leq 0 @i s reálnou neznámou @i\,x.@i
- Řešte nerovnici @i\, (5x-4)^2-(4x-3)^2\leq(2x-5)^2-30\,@i s reálnou neznámou @i\,x.@i
- Řešte nerovnici @i\, \dfrac{5-x}{x-1}+\dfrac{1+4x}{x+1}\leq2\,@i s reálnou neznámou @i\,x.@i
- Řešte nerovnici @i\dfrac{4x+5}{x^2+9}\geq 1 @i s reálnou neznámou @i\,x.@i
Závorku umocníme a všechny členy převedeme na levou stranu nerovnice. Nerovnici vynásobíme @i\, -1@i, aby byl koeficient u @i\,x^2\,@i kladný. Pozor na znaménko!
@b\begin{array}{rcl}-5(1-x)^2&<&3x+11/ -3x-11 \\[2mm] -5(1-2x+x^2)-3x-11&<&0\\[2mm]-5x^2+7x-16&<&0/ \cdot(-1)\\[2mm]5x^2-7x+16&>&0.\end{array}@b
Nejprve musíme najít kořeny rovnice @b 5x^2-7x+16=0.@b Pro rovnici platí @i\ a=5,\ b=-7,\ c=16@i. Vypočteme diskriminant: @i\ D=(-7)^2-4\cdot 5\cdot 16=49-320=-271@i. Rovnice nemá reálné kořeny. Parabola @i\, y= 5x^2-7x+16\,@i je "konvexní" a její vrchol (celá) leží nad osou @i\, x@i. Tedy nerovnost @b 5x^2-7x+16>0@b je splněna pro každé reálné číslo, tj. @i\, K=\mathbb R@i.
Kvadratickou nerovnici bez lineárního členu lze řešit odmocněním, jestliže jsou obě strany nerovnosti nezáporné.
@b \begin{array}{r c l} x^2 -7&\leq&0 \ /+7 \\[2mm] x^2 &\leq&7 /\ \sqrt{\ \, }\\[2mm] \sqrt{x^2}&\leq&\sqrt{7} \\[2mm] |x|&\leq&\sqrt{7}.\end{array}@b Poslední nerovnost říká, že hledáme reálná čísla @i\,x@i, jejichž obraz je vzdálen na číselné ose od nuly o méně než nebo rovno @i\,\sqrt 7@i, tj. @i\,-\,\sqrt 7\leq x\leq \sqrt 7\,@i a @i\,K = \langle -\,\sqrt{7},\sqrt{7}\,\rangle @i.
Pozor, častá chyba: Při odmocňování kvadratické nerovnice používáte nesprávný (nesmyslný) zápis, viz @b \begin{array}{r c l} x^2 &\leq&7 /\ \sqrt{\ \, }\\[2mm] \sqrt{x^2}&\leq&\sqrt{7} \\[2mm] x&\leq&\pm \sqrt{7}.\end{array}@b
Závorky umocníme a všechny členy převedeme na levou stranu nerovnice.
@b\begin{array}{rcl}(5x-4)^2-(4x-3)^2&\leq&(2x-5)^2-30 \\[2mm] 25x^2-40x+16-(16x^2-24x+9)&\leq&4x^2-20x+25-30/ \,-4x^2+20x+5\\[2mm]5x^2+4x+12&\leq&0.\end{array}@b
Nejprve musíme najít kořeny rovnice @b 5x^2+4x+12=0.@b Pro rovnici platí @i\ a=5,\ b=4,\ c=12@i. Vypočteme diskriminant: @i\ D=(4)^2-4\cdot 5\cdot 12=16-240=-224@i. Rovnice nemá reálné kořeny. Parabola @i\, y= 5x^2+4x+12\,@i je "konvexní" a její vrchol (celá) leží nad osou @i\, x@i. Tedy nerovnost @b 5x^2+4x+12\leq 0@b není nikdy splněna, tj. @i\, K=\emptyset@i.
Dvojku odečteme. Na levé straně zlomky sečteme a obdržíme nerovnici v podílovém tvaru.
@b\begin{array}{rcl} \dfrac{5-x}{x-1}+\dfrac{1+4x}{x+1}&\leq&2/ -2 \\[2mm] \dfrac{(5-x)(x+1)+(1+4x)(x-1)-2(x-1)(x+1)}{(x-1)(x+1)}&\leq&0\\[2mm] \dfrac{5x+5-x^2-x+x-1+4x^2-4x-2x^2+2}{(x-1)(x+1)}&\leq&0\\[2mm] \dfrac{x^2+x+6}{(x-1)(x+1)}&\leq&0.\end{array}@b
Nejprve musíme najít kořeny rovnice @b x^2+x+6=0.@b Pro rovnici platí @i\ a=1,\ b=1,\ c=6@i. Vypočteme diskriminant: @i\ D=1^2-4\cdot 1\cdot 6=1-24=-23@i. Rovnice nemá reálné kořeny. Parabola @i\, y= x^2+x+6\,@i je "konvexní" a její vrchol (celá) leží nad osou @i\, x@i. Tedy platí @b x^2+x+6>0@b pro každé reálné číslo. Odtud plyne, že zlomek @i\,\dfrac{x^2+x+6}{(x-1)(x+1)}\,@i není nikdy roven @i\, 0\,@i a je záporný, pokud je záporný jmenovatel, tj. @b(x-1)(x+1)<0. @b Obdrželi jsme nerovnici v součinovém tvaru. Můžeme použít metodu nulových bodů. Využijme geometrický význam nerovnice. Parabola @i\,y=(x-1)(x+1)@i, resp. @i\,y=x^2-1\,@i protne osu @i\, x\,@i v bodech @i\,x=-1, x=1@i. Je "konvexní". Část paraboly, která leží pod osou @i\, x\,@i odpovídá intervalu @i\,(-1,1)@i, tj. řešením zadané nerovnice je interval @i\, K=(-1,1)@i.
Obě strany nerovnice vynásobíme kladným výrazem @i\, x^2+9@i. Parabola @i\,y=x^2+9\,@i leží celá nad osou @i\,x@i. Všechny členy převedeme na pravou stranu nerovnice a strany zaměníme. Na levou stranu nerovnice použijeme vzorec @i\, A^2-2AB+B^2=(A-B)^2@i. @b \begin{array}{r c l} \dfrac{4x+5}{x^2+9}&\geq&1 \ /\cdot(x^2+9) \\[2mm] 4x+5 &\geq&x^2+9\ / -4x-5\\[2mm] 0&\geq&x^2-4x+4 \\[2mm] x^2-4x+4&\leq&0 \\[2mm] (x-2)^2&\leq&0.\end{array}@b Nerovnici vyhovuje jediné @i\,x=2@i, tj. řešením je jednoprvková množina @i\,K = \{2\} @i.
Užitečná poznámka: Připomeňme si, že @i\, A^2=0\,@i právě tehdy, když @i\, A=0@i. Pro každé @i\, A\neq 0@i platí @i\,A^2>0@i.
Neřešené příklady
- Řešte nerovnici @i x^2+3x+4\geq 0 .@i
- Řešte nerovnici @i1> x(1+2x) .@i
- Řešte nerovnici @i 3-\dfrac{x^2-3{,}6x}{2} \geq \dfrac{3x+50}{10} .@i
