Odmocnina, grafické řešení rovnic a nerovnic s odmocninou
Odmocnina, grafické řešení rovnic a nerovnic s odmocninou

Teoretické minimum
Uvažujme kvadratickou funkci @i\,f(x)=x^2\,@i na intervalu @i\,\langle 0,\infty)@i. Grafem je jen polovina paraboly, viz obrázek:
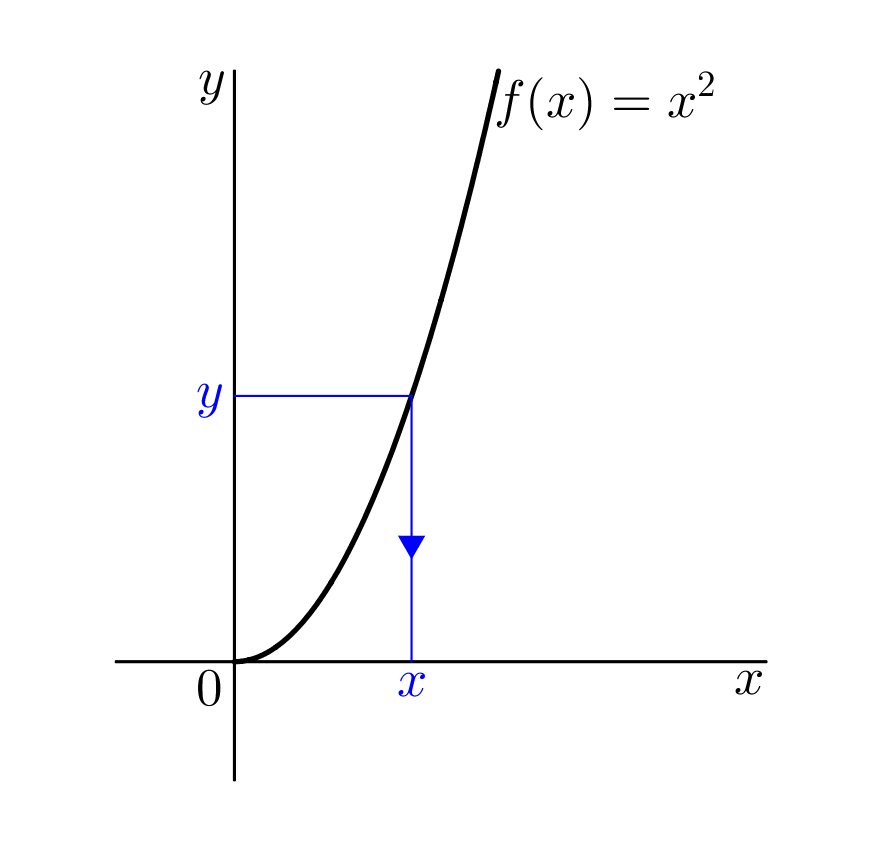
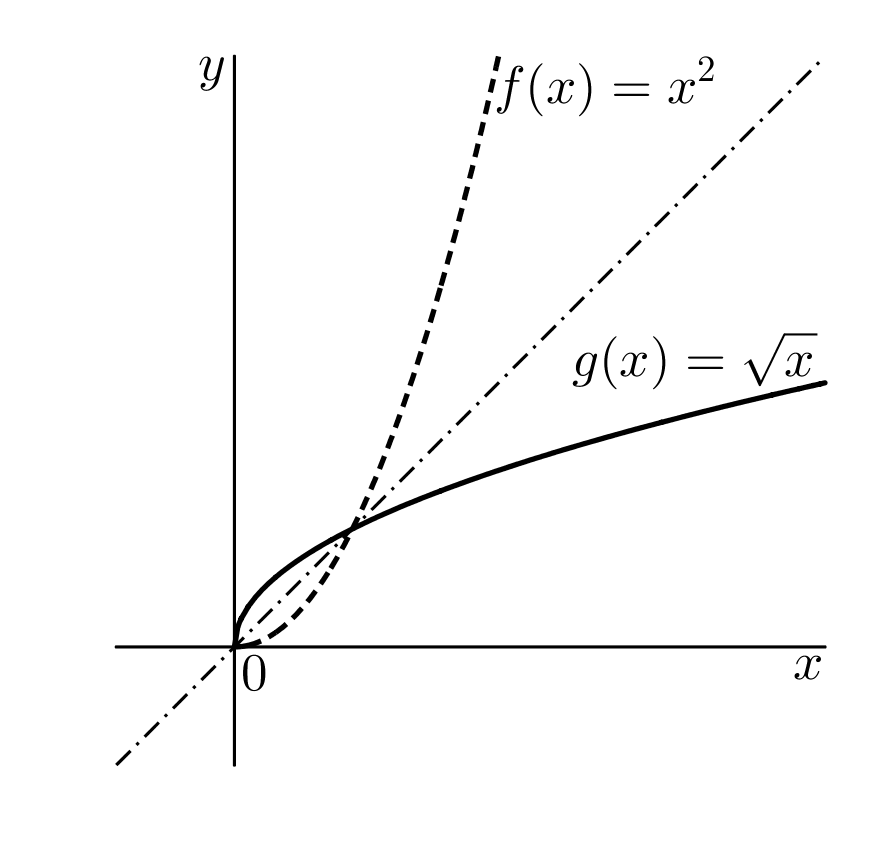
Omezením definičního oboru na nezáporná čísla jsme zajistili, že každé funkční hodnotě @i\,y\geq 0\,@i je přiřazeno právě jedno @i\,x@i. Tento nový funkční předpis nazýváme druhá odmocnina. Budeme psát @i\,g(y)=\sqrt y,\ y\in\langle 0, \infty)@i. Grafem funkce @i\,g\,@i jsou uspořádané dvojice @i\,(y,\sqrt y)@i. Nezávisle proměnnou označíme tradičně @i\,x@i, tedy @b g(x)=\sqrt x.@b Graf funkce @i\,g\,@i je symetrický s grafem funkce @i\,f\,@i podle osy 1. a 3. kvadrantu, viz obrázek:
Užitečná poznámka: Stejnou úvahou získáme z ostatních sudých mocnin předpisy sudých odmocnin. Jejich grafy jsou kvalitativně stejné, viz obrázek:
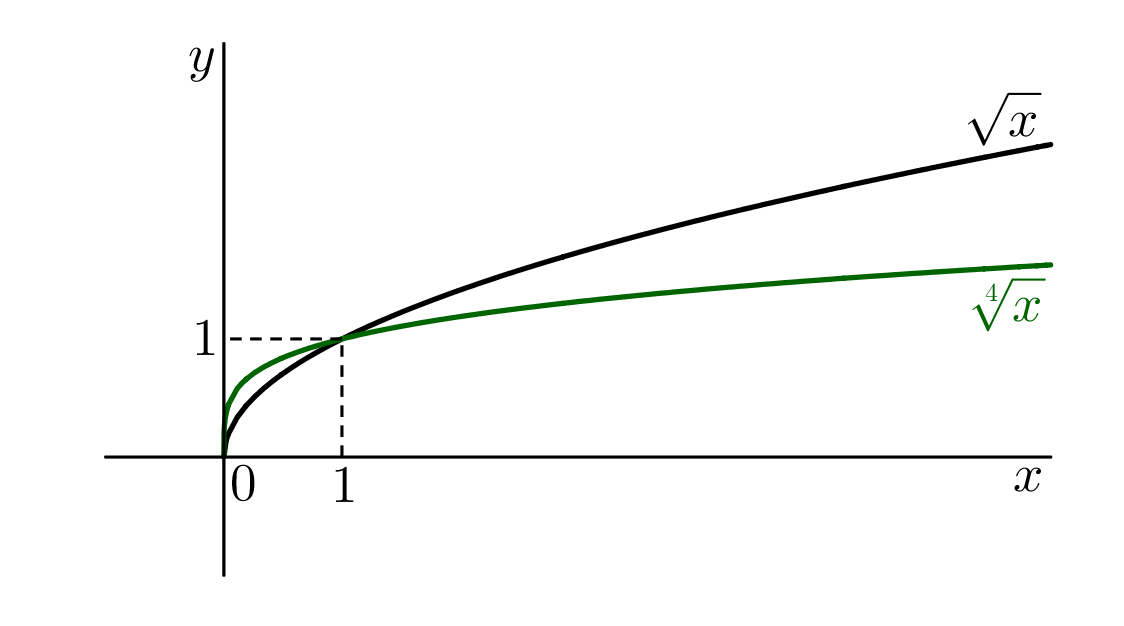
Funkce druhá (resp. sudá) odmocnina @b g(x)=\sqrt[2k] x,\ k\in\mathbb N @b má za definiční obor nezáporná čísla, tj. @b\mathcal D(g)=\langle 0,\infty).@b Graf funkce @i\,g\,@i leží v polorovině @i\,y\geq 0@i, tj. @b\mathcal H(g)=\langle 0,\infty).@b
Uvažujme nyní funkci @i\,f(x)=x^3@i. Grafem je kubická parabola, viz obrázek:
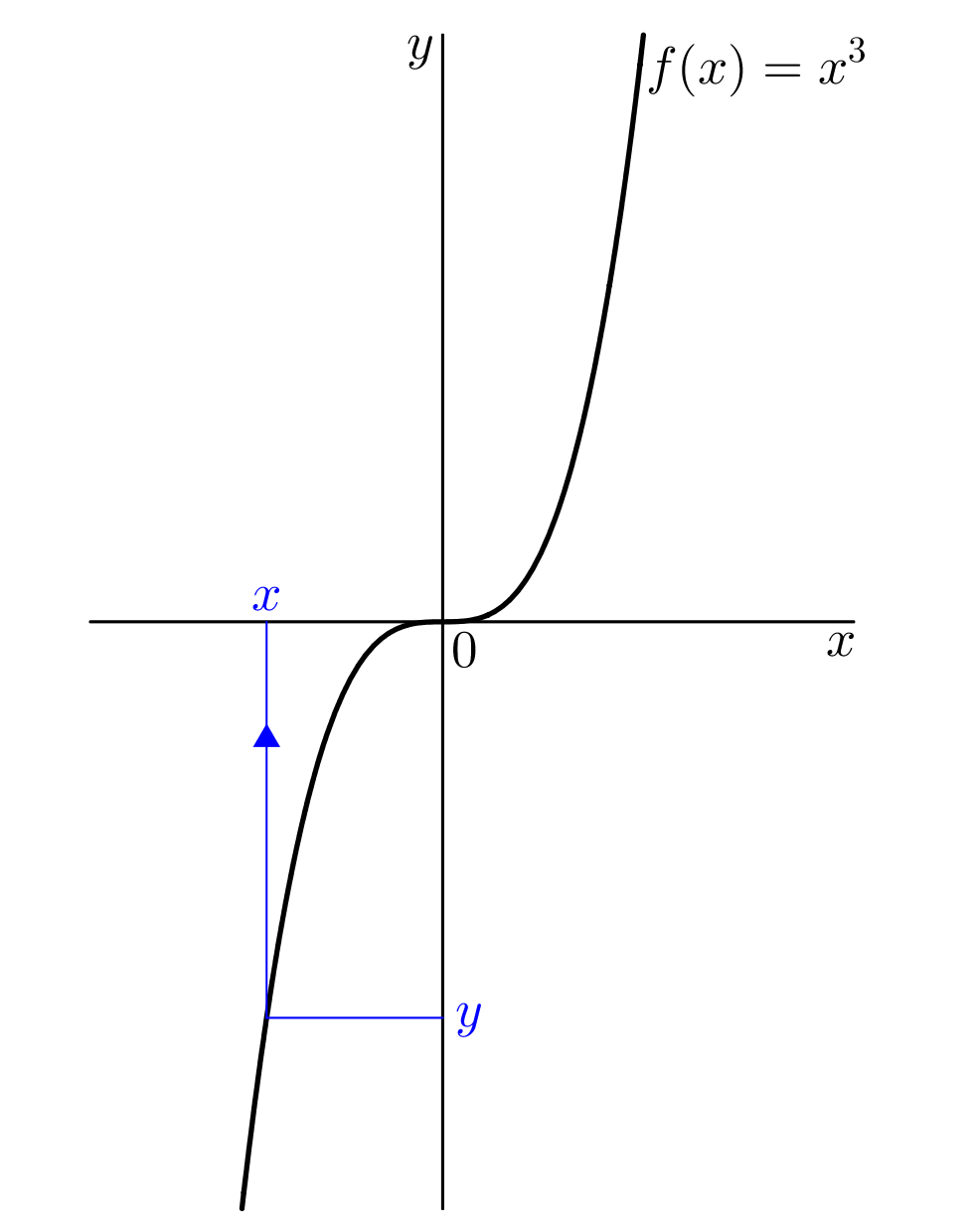
Pro všechna reálná @i\,x\,@i má funkce @i\,f\,@i vlastnost, že pro každou funkční hodnotu @i\,y\,@i existuje právě jedna nezávislá proměnná @i\,x@i. Tento nový funkční předpis nazýváme třetí odmocnina. Píšeme @i\,g(y)=\sqrt[3] y,\ y\in\mathbb R@i. Nezávisle proměnnou označíme @i\,x@i, @b g(x)=\sqrt[3] x .@b Definičním oborem na rozdíl od druhé mocniny je každé reálné číslo, tj. @b\mathcal D(g)=\mathbb R.@b Grafy funkcí @i\,f\,@i a @i\,g\,@i jsou symetrické podle osy 1. a 3. kvadrantu, viz obrázek:
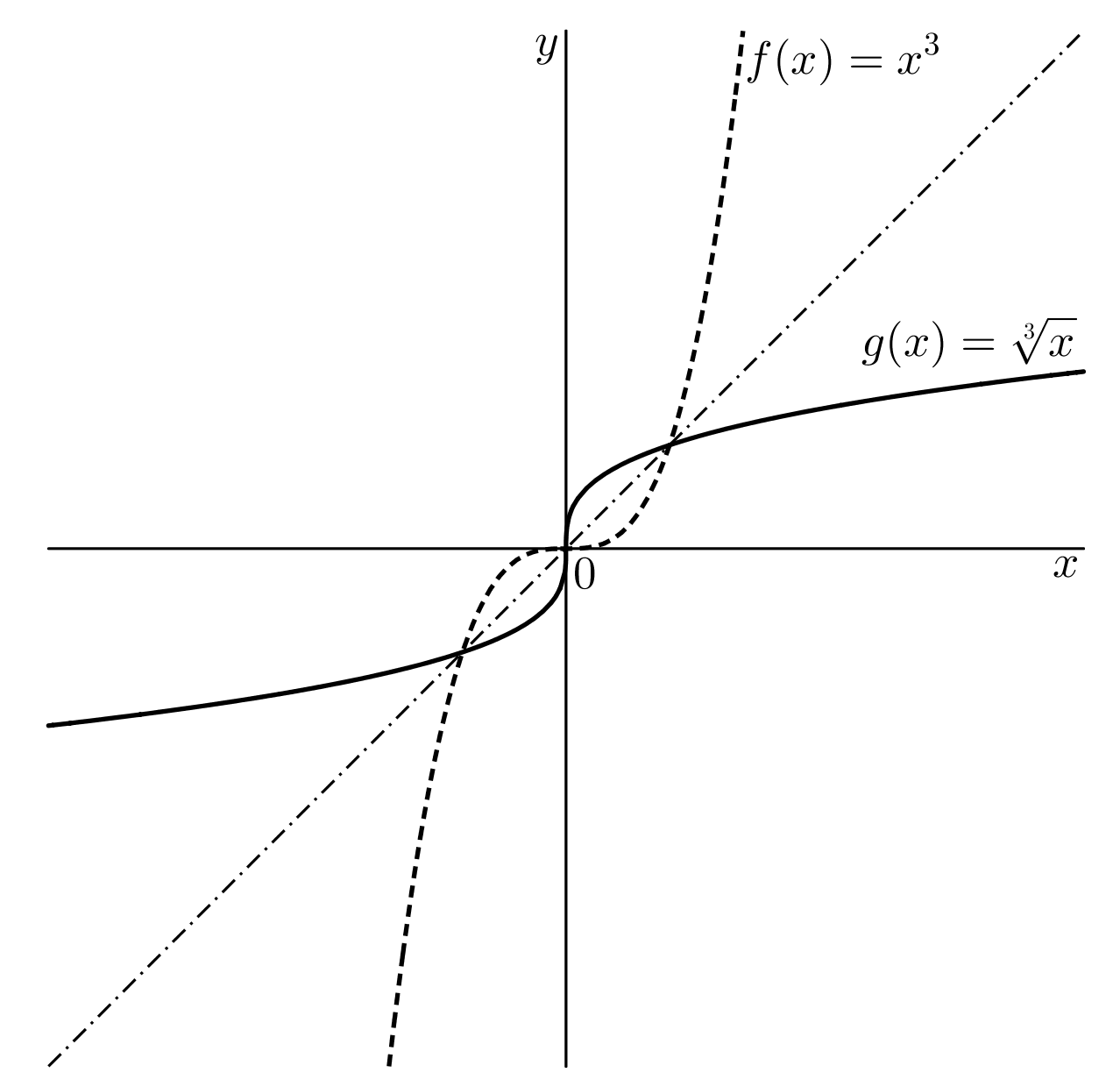
Užitečná poznámka: Stejnou úvahou získáme z ostatních lichých mocnin předpisy lichých odmocnin. Jejich grafy jsou kvalitativně stejné, viz obrázek:

Funkce třetí (resp. lichá) odmocnina @b g(x)=\sqrt[2k+1] x,\ k\in\mathbb N @b má za definiční obor všechna reálná čísla, tj. @b\mathcal D(g)=\mathbb R @b a obor hodnot snadno vyčteme z obrázku @b\mathcal H(g)=\mathbb R.@b
Související
Mocniny a odmocniny, Ekvivalentní úpravy, Definiční obor funkce.
Řešené příklady
- Určete definiční obor funkce @i\ f(x) = \sqrt{ 3-\sqrt{x+1}}@i.
- Určete definiční obor funkce @i\ f(x) =\arccos \sqrt{ x+2}@i.
- Řešte v oboru reálných čísel rovnici @i\ \sqrt{x+5}=x-1@i.
- Řešte v oboru reálných čísel rovnici @i\ \sqrt{2x+1}+\sqrt{x-3}=2\,\sqrt x@i.
- Řešte v oboru reálných čísel nerovnici @i\ 3 \sqrt[3]{x+1}+\sqrt{36}<0@i.
- Graficky řešte nerovnici @i\ \sqrt{x+4}>x+2@i.
Potřebujeme zajistit, aby výrazy pod odmocninami byly nezáporné, tj. @b x+1\geq 0\qquad \wedge\qquad 3-\sqrt{x+1} \geq 0.@b První nerovnice je splněna pro @ix\geq-1@i. Upravujme druhou (umocnění je ekvivalentní úpravou, neboť obě strany nerovnice jsou nezáporné):
@b\begin{array}{r c l}3-\sqrt{x+1}&\geq & 0 \\ 3&\geq & \sqrt{x+1} \\ 9&\geq & x+1\\ 8&\geq & x \end{array}@b Obě podmínky jsou splně pro @i\,x\in\langle -1,8\rangle@i, tj. definiční obor funkce @i\,f\,@i je @b D(f) = \langle -1,8 \rangle.@b
Definiční obor funkce arccosinus je uzavřený interval @i\,\langle -1,1\rangle@i a dále pod odmocninou nesmí být záporné číslo. Máme následujíí podmínky: @b x+2\geq 0\qquad \wedge \qquad -1\leq\sqrt{x+2} \leq 1.@b Soustavu nerovnic budeme řešit graficky. Označme odmocninu jako funkci @i\,g@i, tj. @i\,g(x)=\sqrt{x+2}@i. Graf druhé odmocniny posuneme ve směru osy @i\,x\,@i o dvě jednotky doleva. Dále do obrázku zakreslíme dvě konstatní funkce @i\,\pm 1@i, viz obrázek:
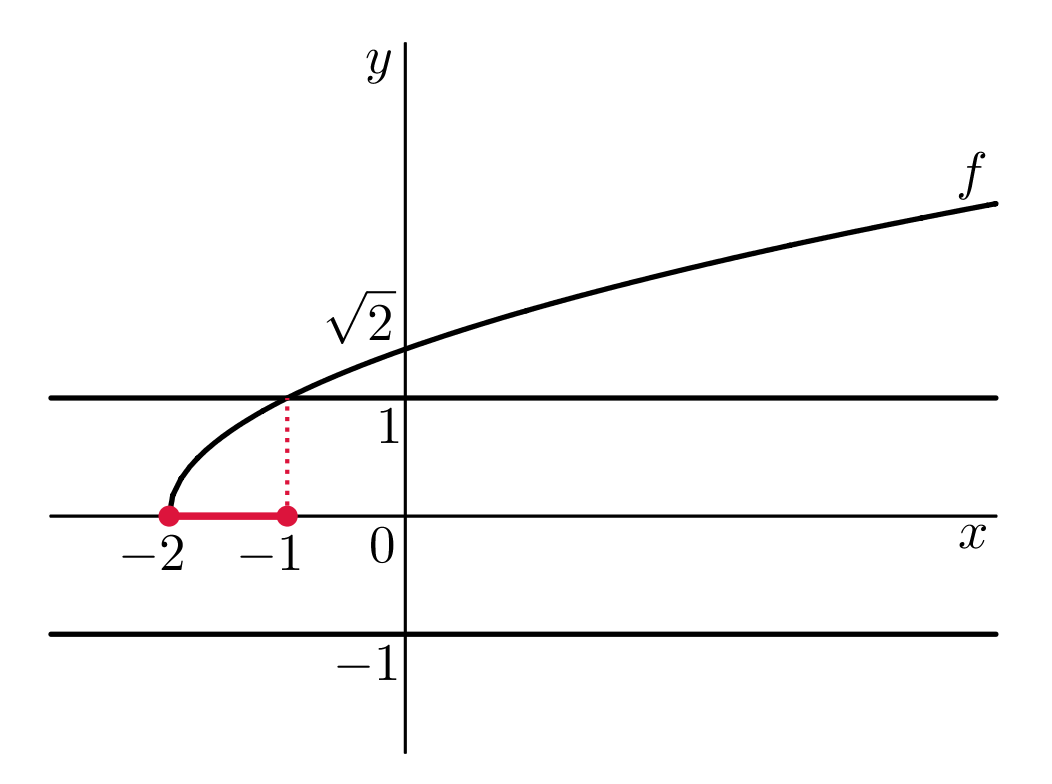
Z obrázku je vidět, že nerovnost @i\,-1\leq \sqrt{x+2}\,@i je splně vždy. Zbývá dopočítat průsečík grafu funkce @i\,g\,@i a konstantní jedničky. Řešme rovnici:
\sqrt{x+2}&= & 1 \\ x+2&= &1 \\ x&= & -1\end{array}@b Definiční obor funkce @i\,f\,@i nyní snadno vyčteme z obrázku. @b D(f) = \langle -2,-1 \rangle.@b
Pozor, častá chyba: Soustavu nerovnic lze řešit algebraicky. Nelze však postupovat takto: @b\begin{array}{r c l}
-1\leq \sqrt{x+2}&\leq & 1 \\ (-1)^2\leq\Bigl(\sqrt{x+2}\Bigr)^2&\leq& 1^2 \\ 1\leq x+2&\leq&1 \end{array}@b Nerovnost @i\,-1\leq\sqrt{x+2}\,@i je splněna vždy, když odmocnina existuje. Tedy @i\,x\geq-2@i. Funkční hodnoty odmocniny jsou nezáporná čísla. Úpravu umocnění obou stran nerovnice nelze použít! U druhé nerovnice umocnění můžeme použít. Obě strany nerovnice jsou nezáporné, tj. @b\begin{array}{r c l}
\sqrt{x+2}&\leq & 1 \\ x+2&\leq&1 \\ x&\leq&-1. \end{array}@b
Nerovnice má smysl pro všechna @ix\geq -5.@i Umocníme obě strany rovnice. Úprava není ekvivalentní. Je třeba udělat zkoušku.
\sqrt{x+5}&=& x-1 \\[2mm] x+5&=& (x-1)^2 \\[2mm ] x+5&=&x^2-2x+1 \\[2mm] 0&=& x^2-3x-4\\[2mm] x&\in& \{-1,4\} \end{array}@b Pro @i\,x=-1\,@i je levá strana rovnice rovna @i\,L=\sqrt{-1+5}=2\,@i a pravá strana rovnice rovna @i\,P=-1-1=-2@i. Tedy @i\,x=-1\,@i není řešení rovnice. Pro @i\,x=4\,@i je levá strana rovnice rovna @i\,L=\sqrt{4+5}=3\,@i a pravá strana rovnice rovna @i\,P=4-1=3@i. Tedy @b x=4 @b je jediné řešení rovnice.
Užitečná poznámka: Nakreslete si obrázek s grafem funkce @i\,f(x)=\sqrt{x+2}\,@i a @i\,g(x)=x-1@i. Grafy se protnou právě jednou a to pro @i\,x=4@i.
Nerovnice má smysl, pokud jsou splněný podmínky @i\, x\geq -\,\frac 12\ \wedge\ x\geq3\ \wedge \ x\geq 0.@i Tedy podmínka řešitelnosti nerovnice je @i\,x\geq 3@i. Umocníme obě strany rovnice. Úprava není ekvivalentní. Je třeba udělat zkoušku.
Umocňujeme součet, použijeme vzorec @i\,(A+B)^2=A^2+2AB+B^2@i.
\sqrt{2x+1}+\sqrt{x-3}&=& 2\,\sqrt x \\[2mm] 2x+1+2\,\sqrt{2x+1}\,\sqrt{x-3}+x-3&=& 4x \end{array}@b Odmocniny necháme vlevo a ostaní členy převedeme doprava a opět umocníme.
@b\begin{array}{r c l}
2\,\sqrt{2x+1}\,\sqrt{x-3}&=& x+2 \\[2mm ] 4 (2x+1)(x-3)&=&(x+2)^2 \\[2mm] 4(2x^2-5x-3)&=& x^2+4x+4\\[2mm] 7x^2-24x-16&=&0\\[2mm]x&\in& \left\{-\,\dfrac 47,4\right\} \end{array}@b
Kvadratickou rovnici řešíme pomocí diskriminantu. Kořen @i\,x=-\,\frac 47\,@i nesplňuje podmínku řešitelnosti. Pro @i\,x=4\,@i je levá strana rovnice rovna @i\,L=\sqrt{8+1}+\sqrt{4-3}=3+1=4\,@i a pravá strana rovnice rovna @i\,P=2\,\sqrt 4=4@i. Tedy @b x=4 @b je jediné řešení rovnice.
Pozor, častá chyba: Umocňujeme součet!!! @i\,\Bigl(\sqrt{2x+1}+\sqrt{x-3}\Bigr)^2\,@i se nerovná @i\,\Bigl(\sqrt{2x+1}\Bigr)^2+\Bigl(\sqrt{x-3}\Bigr)^2@i.
Nerovnice má smysl pro všechna @ix\in\mathbb{R}.@i Ekvivalentními úpravami osamostatníme @i\,x\,@i:
@b\begin{array}{r c l}3 \sqrt[3]{x+1}+6&<& 0\ /:3 \\ \sqrt[3]{x+1}+2&<& 0\\ \sqrt[3]{x+1}&<& -2\\ x+1&<& (-2)^3 \\ x&<& -9 \end{array}@b Řešením nerovnice je interval @bK = (-\infty,-9).@b
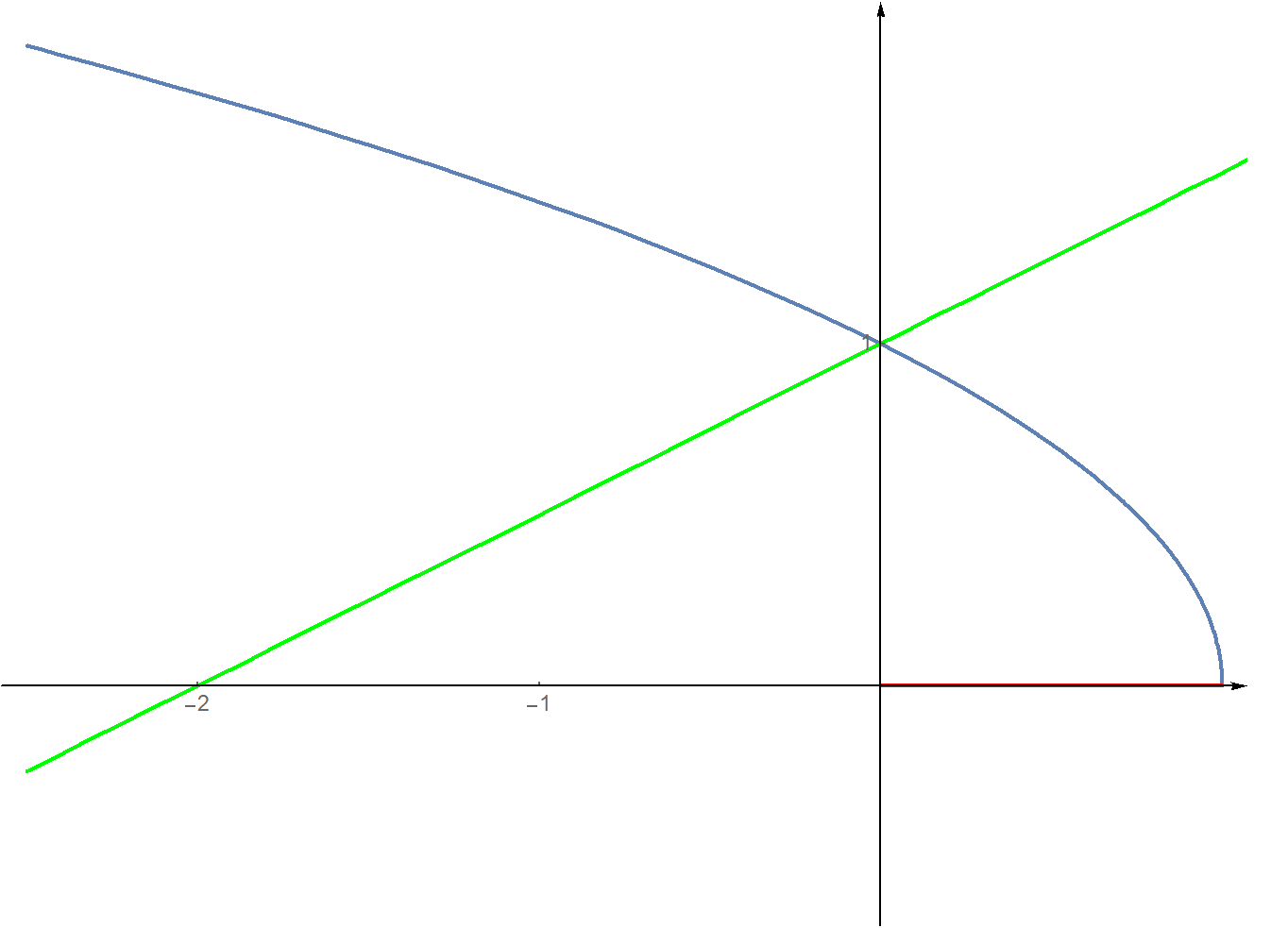
Označme výraz na levé straně rovnice jako předpis funkce @i\,f@i, tj. @i\,f(x)=\sqrt{x+4}\,@i a výraz na pravé straně rovnice jako předpis funkce @i\,g@i, tj. @i\,g(x)=x+2@i
Grafem funkce @i\,f\,@i získáme z grafu odmocniny, který posuneme ve směru osy @i\,x\,@i o čtyři jednotky doleva. Grafam funkce @i\,g\,@i je přímka, viz. obrázek:

Grafy se protnou v jednom bodě @i\,(0,2)@i.
Najít @i\,x@i-ovou souřadnici průsečíku
znamená vyřešit rovnici @i\,\sqrt{x+4}=x+2@i. Rovnice má smysl pro @i\,x\geq-4@i. Rovnici umocníme a upravíme do součinového tvaru: @b\begin{array}{r c l}
\sqrt{x+4}&= &x+2 \\ x+4&=&(x+2)^2 \\ x+4&=&x^2+4x+4\\ 0&=&x^2+3x\\ 0&=&x(x+3)\\ x&\in&\{-3,0\} \end{array}@b Kořen @i\,x=-3\,@i nesplňuje
zkoušku. Z obrázku snadno vyčteme řešení. Řešením zadané nerovnice jsou ta @i\,x@i, pro která graf funkce @i\,f\,@i leží nad grafem funkce @i\,g@i, tj. @b x\in\langle -4,0).@b
Neřešené příklady
- Určete přirozený definiční obor funkce @if(x) = \sqrt[4]{\frac{3}{\sqrt{x}}-2 }@i.
- Řešte nerovnici @i \sqrt[4]{17x^2-34x} < 2\sqrt{x-1}. @i
- Řešte rovnici @i \sqrt[3]{x+1} = 1+\frac{x}{3}. @i
- Řešte graficky nerovnici @i \sqrt{1-x}<\frac{x+2}{2}. @i
- Řešte nerovnici @i \sqrt[3]{3x+8} -x> 2. @i

 @i K = (0,1\rangle@i
@i K = (0,1\rangle@i