Logaritmické funkce, rovnice a nerovnice
Logaritmické funkce, rovnice a nerovnice

Teoretické minimum
Logaritmus kladného čísla @i\,y\,@i při kladném základu @i\,a\,@i různém od jedné (zapisujeme @i\,\log_ay\,@i) je takové číslo (exponent) @i\,x@i, kterým musíme umocnit základ @i\,a@i, abychom dostali dané číslo @i\,y@i. Pro @i\,a>0\ \wedge a\neq1\,@i a @i\,y>0\,@i platí @b x=\log_ay\qquad\Longleftrightarrow \qquad y=a^x@b Při výpočtu logaritmu si říkáme @i\,a\,@i na kolikátou je @i\,y@i.
Například @b\begin{array}{rl}& \log_2 8=3,\quad \textrm{protože} \quad 2^3=8\\[2mm] & \log_{\frac 12}4=-2,\quad \textrm{protože} \quad \left(\frac 12\right)^{-2}=4\end{array}@b Dvě na kolikátou je @i8@i, jedna polovina na kolikátou jsou @i4@i. Pro @i\,a>0\ \wedge a\neq1\,@i je @b\begin{array}{rl}&\log_a a=1,\\[2mm]&\log_a1=0,\\[2mm] &\log_a a^x=x.\end{array}@b Logaritmus, který má za základ Eulerovo číslo @i\,\mathrm{e}\,@i (viz exponenciální funkce), nazýváme přirozený logaritmus a zavádíme pro něj označení @b\log_{\mathrm{e}}x=\ln x.@b Logaritmus, který má za základ konstantu @i10@i, nazýváme dekadický logaritmus a zavádíme pro něj označení @b \log_{10}x=\log x.@b
Pravidla logaritmování
Předpokládejme, že současně platí podmínky:@i\ a>0,\ b>0,\ z>0,\ z\neq1@i. Potom
1. Logaritmus součinu kladných čísel je roven součtu jejich logaritmů: @b\log_z ab=\log_z a+\log_z b.@b
2. Logaritmus podílu kladných čísel je roven rozdílu logaritmů dělence a dělitele: @b\log_z \frac ab=\log_z a-\log_z b.@b
3. Logaritmus mocniny s kladným základem je roven součinu mocnitele a logaritmu základu mocniny: @b\log_z a^k=k\cdot \log_z a, \quad k\in\mathbb{R}.@b
4. Logaritmus @i\,n@i-té odmocniny, @i\,n\,@i je přirozené číslo: @b \log_z\sqrt[n] a=\log_z a^{\frac 1n}=\frac 1n\cdot \log_z a.@b
5. Přímo z definice plyne: @ba^{\log_ab}=b.@b
Logaritmická funkce je každá funkce daná předpisem @b f(x)=\log_a{x},\quad a>0\ \wedge \ a\neq1.@b Číslo @i\,a\,@i se nazývá základ logaritmické funkce. Je pevně dané a je buď větší než @i 1@i nebo @i\,a\in(0,1)@i. Výraz @i\,\log_ax\,@i má smysl jen pro kladná @i\,x@i. Definiční obor logaritmické funkce: @b\mathcal D(f)=(0,\infty).@b
Užitečná poznámka: Logaritmická funkce @i\,f(x)=\log_a x\,@i je funkce inverzní k exponenciální funkci @i\,g(x)=a^x@i, viz inverzní funkce.
Grafem logaritmické funkce je logaritmická křivka, viz následující obrázek:

kde @i\, a>1@i. Pro @i\,a>0\ \wedge \ a\neq1\,@i platí @i\,\log_ax=-\log_{\frac 1a}x @i. Z čehož plyne (viz graf funkce), že grafy logaritmických funkcí @i\,\log_ax\,@i a @i\,\log_{\frac 1a}x\,@i jsou vzájemně symetrické podle osy @i\,x@i, viz následující dva obrázky:
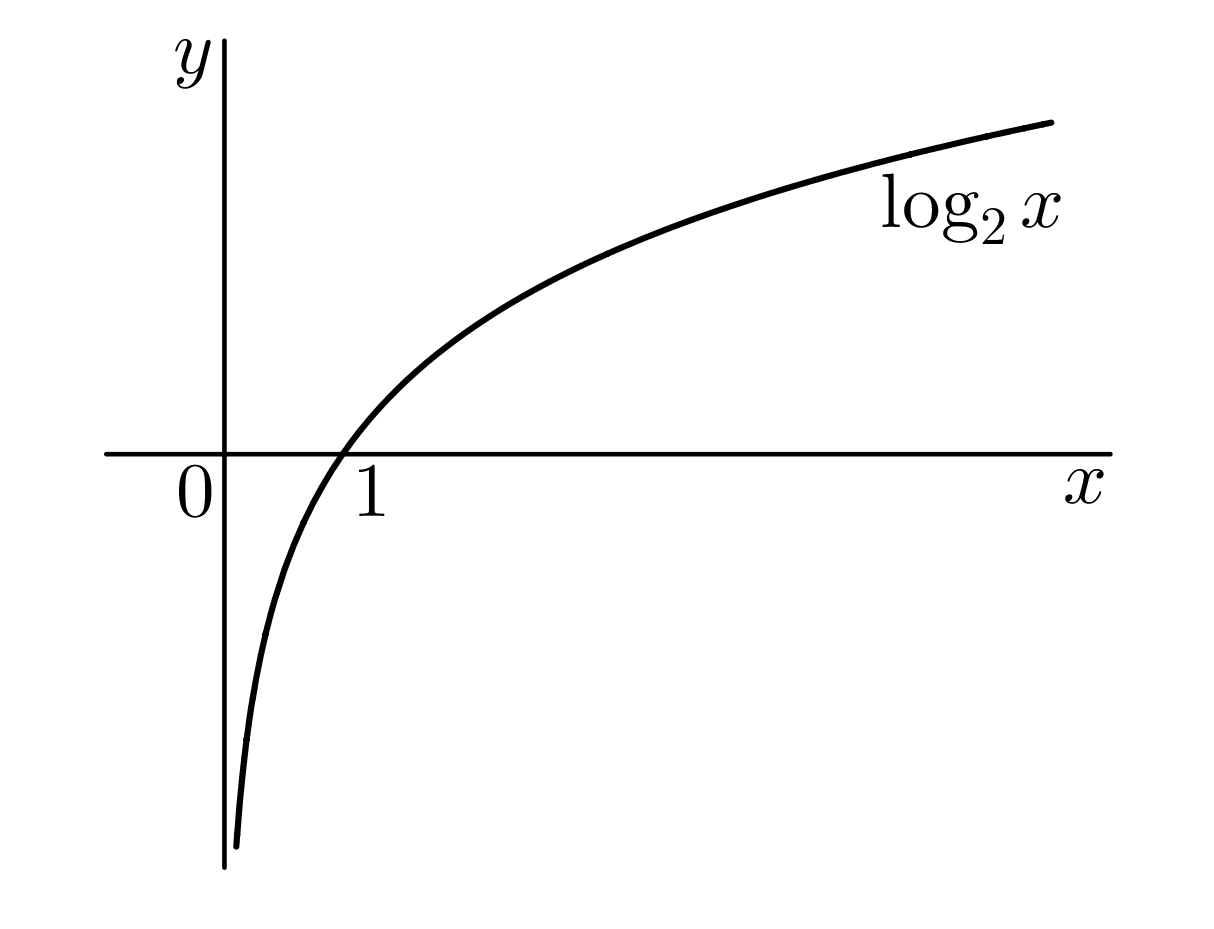
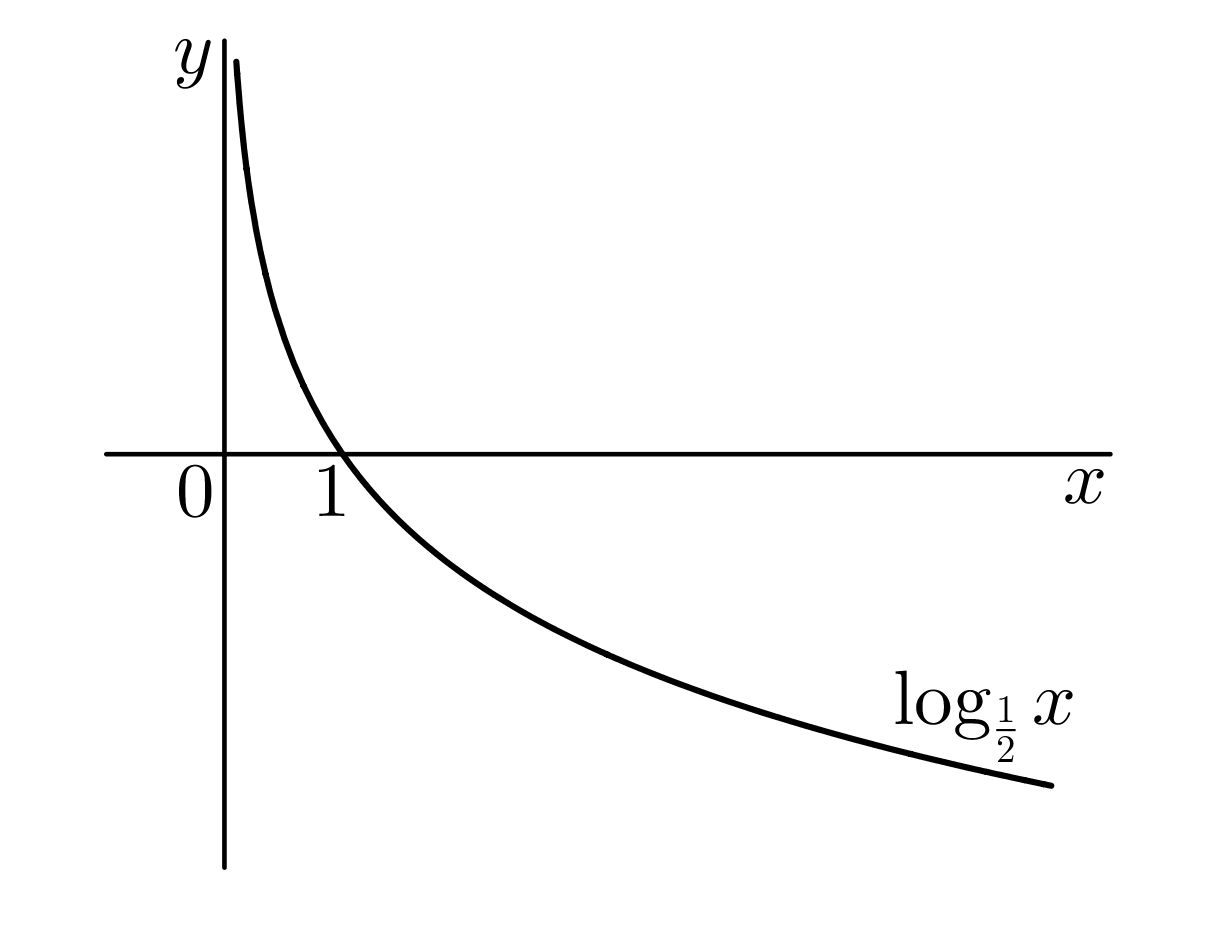
Z obrázků vidíme, že obor hodnot logaritmické funkce jsou všechna reálná čísla, tj. @b\mathcal H(f)=\mathbb{R}.@b
Užitečná poznámka: Logaritmická funkce @i\,f(x)=\log_ax@i, kde @i\,a>1\,@i je rostoucí. Je-li @i\,a\in(0,1)@i, je logaritmická funkce @i\,f(x)=\log_ax\,@i klesající.
Při řešení logaritmických rovnic využijeme důležitou vlastnost logaritmické funkce. Pro @i\, a>0\ \wedge \ a\neq1\,@i platí @b \log_ax=\log_ay\quad \Longrightarrow\quad x=y.@b Vlastnosti říkáme, že logaritmická funkce je
prostá.
Při řešení logaritmických nerovnic využijeme jinou vlastnost logaritmické funkce. Pro @i\, a>1\,@i platí @b \log_ax>\log_ay\quad \Longrightarrow\quad x>y.@b Vlastnosti říkáme, že logaritmická funkce o základu větším než @i\,1\,@i je rostoucí. Pro @i\, a\in(0,1)\,@i platí @b \log_ax>\log_ay\quad \Longrightarrow\quad x<y.@b Vlastnosti říkáme, že logaritmická funkce o kladném základu menším než @i\,1\,@i je klesající.
Související
Kvadratická nerovnice, nerovnice v součinově-podílovém tvaru, definiční obor funkce.
Řešené příklady
- Určete přirozený definiční obor funkce @i\ f(x)= \dfrac{x}{\log_2 x-4}@i.
- Určete přirozený definiční obor funkce @i\ f(x)= \dfrac{1}{\sqrt{\log x-1}}@i.
- Řešte rovnici @i\ \log(x^2+7x)=1+\log(x+1)\, @i v množině reálných čísel. Rovnice má smysl pro všechna reálná @i\,x\,@i splňující podmínky: @b\begin{array}{rcl} x^2+7x>0\quad &\wedge&\quad x+1>0 \\ x(x+7)>0\quad &\wedge&\quad x>-1\\ x\in(-\infty,-7)\cup(0,\infty)\quad &\wedge&\quad x\in(-1,\infty)\end{array}@b tj. @b x\in(0,\infty).@b Rovnici převedeme do tvaru @i\,\log f(x)=\log g(x)@i, pak @i\,f(x)=g(x)@i. Použijeme pravidlo součet logaritmů je logaritmus součinu. @b \begin{array}{r c l} \log(x^2+7x)& = & 1+\log(x+1) \\ \log(x^2+7x)& = & \log 10+\log(x+1) \\ \log(x^2+7x)& = & \log \bigl(10(x+1)\bigr) \\ x^2+7x& = & 10(x+1) \\ x^2-3x -10 & = &0 \end{array} @b Kvadratická rovnice má dvě řešení @i \, x_1=5\, @i a @i\, x_2=-2,@i ale @i\, -2\notin (0,\infty)@i. Řešením zadané rovnice je pouze @i\,x=5@i, tj. @bK=\{5\}.@b Pozor, častá chyba: Na začátku zapomenete udělat podmínky řešitelnosti rovnice a hned se pustíte do řešení.
- Řešte nerovnici @i\ \log_{\frac13}(x+1)+1>0 \,@i v množině reálných čísel. Nerovnice má smysl pro všechna reálná @i\,x\,@i splňující podmínku: @i\, x+1>0@i, tj. @i\,x\in(-1,\infty).@i @b\begin{array}{r c l} \log_{\frac 13}(x+1)+1&>&0\\ \log_{\frac13}(x+1)&> & -1 \\ \log_{\frac13}(x+1)&> & \log_{\frac13} 3 ,\qquad (\bigl(\frac13\bigr)^{-1}=3) \\ x+1&< & 3 \qquad (\text{základ je menší než jedna, funkce je klesající, otáčíme znaménko})\\ x&< & 2 \end{array} @b Řešením nerovnice je tedy @bK= (-1,2) .@b Pozor, častá chyba: Na závěr zapomenete zahrnout podmínku řešitelnosti nerovnice, tj. udělat průnik intervalů @i\,(-1,\infty)@i a @i\,(-\infty,2)@i.
- Řešte nerovnici @i\ \dfrac{\ln x (2-\ln x )}{x-2} \geq 0\,@i v množině reálných čísel. Nerovnice má smysl pro všechna reálná @i\,x\,@i splňující podmínky: @i\,x>0\ \wedge\ x\neq0@i, tj. @i x\in(0,2)\cup (2,\infty).@i Nerovnice je v součinově-podílovém tvaru. Vyšetříme znaménko každého činitele zvlášť. Nulové body jsou @i\, x=1\, @i pro @i\,\ln x@i, @ix=\mathrm{e}^2@i pro @i\,2-\ln x\,@i a @i\,x=2\,@i pro @i\,x-2.@i Množinu kladných čísel rozdělí na čtyři intervaly, pro které platí: @b \begin{array}{|c|c|c|c|c|c|c|c|} \hline (0,2)\cup (2,\infty)&& (0,1 )& 1 & (1,2)& \bigl(2,\mathrm{e}^2\bigr) &\mathrm{e}^2 & \bigl(\mathrm{e}^2,\infty\bigr)\\ \hline \ln x && - & 0 & + & + & + & + \\ \hline 2-\ln x && +& + &+ & + & 0& - \\ \hline x-2 && -& - & - & + & +& +\\ \hline \frac{\ln x (2-\ln x )}{x-2} && \boldsymbol{+}& \bf{0}&{\bf -} &{\bf +} & {\bf 0} & {\bf -}\\ \hline \end{array} @b Z tabulky snadno vyčteme, že podíl je nezáporný pro @i\,x\in(0,1\rangle \cup (2,\mathrm{e}^2\rangle@i, tedy @b K= (0,1\rangle \cup (2,\mathrm{e}^2\rangle .@b
- Řešte nerovnici @i\ \mathrm{e}^x+\mathrm{e} < \mathrm{e}^2\, @i v množině reálných čísel. Osamostatníme přirozenou exponenciálu. @b \begin{array}{r c l} \mathrm{e}^x+\mathrm{e}&< & \mathrm{e}^2 \\[2mm] \mathrm{e}^x & < & \mathrm{e}^2 - \mathrm{e} \end{array}@b Neboť je @i\, \mathrm{e}^2 - \mathrm{e}>0@i, můžeme na obě strany nerovnice použít funkci přirozený logaritmus. Platí @i\,\ln\mathrm{e}^x=x @i. Tedy @b\begin{array}{rcl} x & < & \ln( \mathrm{e}^2 - \mathrm{e} )\\ x & < & \ln\bigl( \mathrm{e}(\mathrm{e}-1)\bigr)\\ x & < & \ln \mathrm{e} + \ln(\mathrm{e}-1)\\ x & < & 1 + \ln(\mathrm{e}-1) \end{array}@b Množina všech řešení je: @b K= \bigl(-\infty, 1 + \ln(\mathrm{e}-1) \bigr) @b
- Graficky řešte nerovnici @i\, \log_2(x+1)< \mathrm{e}^{-x}-1@i. Označme funkci na levé straně nerovnice písmenkem @i\,f@i, tj. @i\, f(x)= \log_2(x+1)\,@i a funkci na pravé straně písmenkem @i\,g@i, tj. @i\,g(x)=\mathrm{e}^{-x}-1=\left(\dfrac 1{\mathrm{e}}\right)^x-1 @i. Do jednoho obrázku zakreslíme graf funkce @i\,f\,@i a graf funkce @i\,g@i. Grafem funkce @i\,f\,@i je logaritmická křivka posunutá o jednu jednotku doleva ve směru osy @i\, x\,@i procházející bodem @i\,(0,0)@i. Grafem funkce @i\,g\,@i je exponenciální křivka posunutá o jednu jednotku dolů ve směru osy @i\, y\,@i procházející bodem @i\,(0,0)@i, viz obrázek:
Vypíšeme podmínky, za kterých má výraz @i\,\dfrac x{\log_2 x-4}\,@i smysl: @i x>0 \:\:\wedge\:\:\log_2 x-4\neq 0@i.
@b \begin{array}{r c l} \log_2 x-4& \neq & 0 \\ \log_2 x& \neq & 4 \\ x& \neq & 2^4 \end{array}@b Druhá podmínka je splněna pro @i x\neq 16 @i, celkem tedy @b \mathcal D(f) = (0,16)\cup (16,\infty). @bVypíšeme podmínky, za kterých má výraz @i\,\dfrac 1{\sqrt{\log x-1}}\,@i smysl: @i \sqrt{\log x-1}\neq 0 \:\:\wedge\:\:\log x-1\geq 0 \:\:\wedge\:\: x> 0@i. Druhá odmocnina nabývá hodnotu nula je pro nulu, tedy @i\,\log x-1\neq 0@i. Přidáme-li k této podmínce druhou podmínku musí platit, že @b \log x-1>0.@b Řešme nerovnici graficky. Graf dekadického logaritmu posuneme ve směru osy @i\,y\,@i o jednotku dolů. Graf funkce @i\,f(x)=\log x-1\,@i protíná osu @i\,x\,@i v bodě @i\,(10,0)@i, viz obrázek:

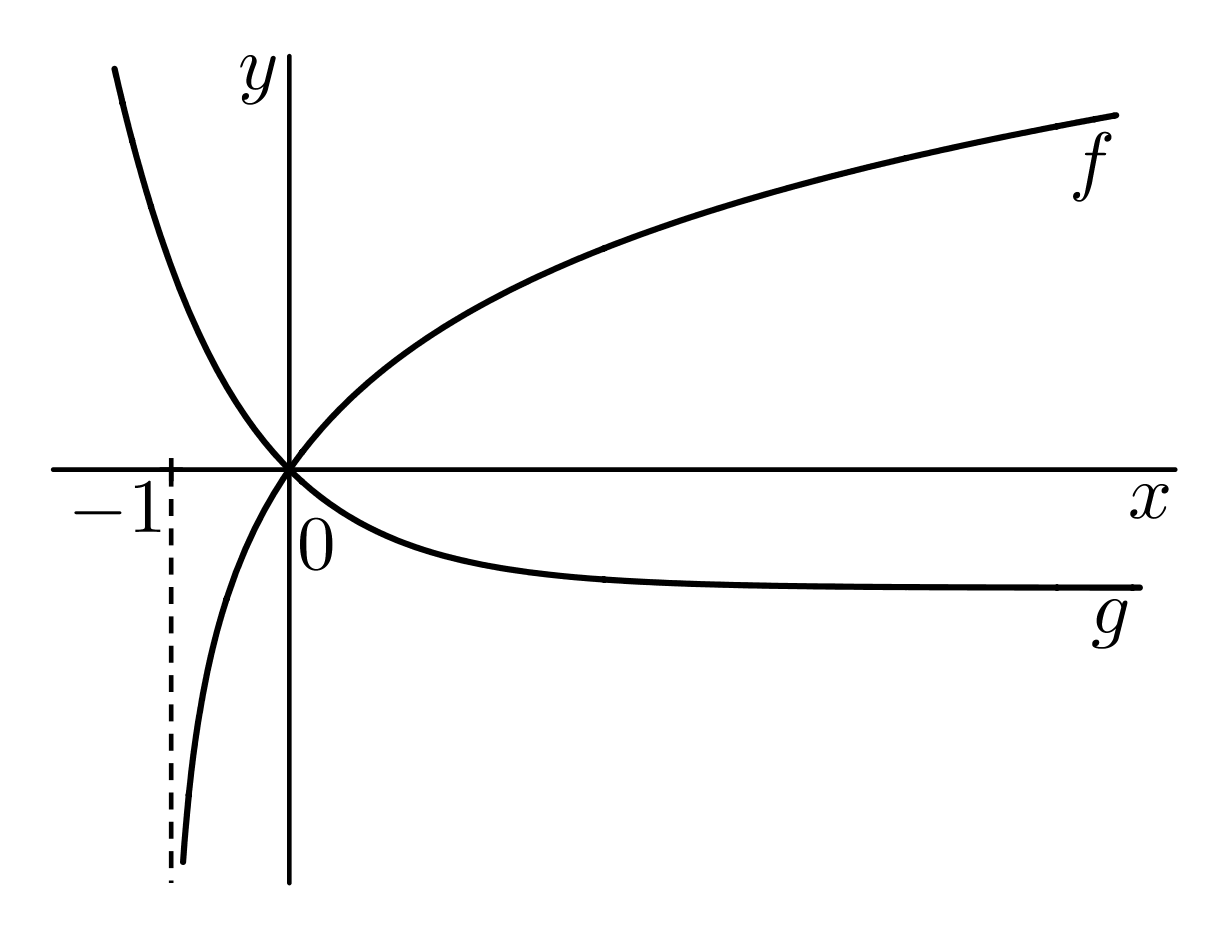
Z obrázku je patrné, že @i\,f(x)<g(x)\,@i pro všechna @i\,x\in(-1,0)@i. Tedy řešením nerovnice je interval @i\,K=(-1,0)@i.
Neřešené příklady
- Určete přirozený definiční obor funkce @i f(x)= \ln\bigl(2-\log(x+1)\bigr) @i.
- Řešte graficky rovnici @i x^3 + \log_{\frac12}(x+1)=0 @i.
- Řešte rovnici @i 1 = \ln(x)- \ln (2x-3) @i.
- Řešte nerovnici @i \dfrac{x(1+\log x )}{\log (2x)} \leq 0 @i.
