Lineární lomená funkce, grafické řešení rovnic a nerovnic
Lineární lomená funkce, grafické řešení rovnic a nerovnic

Teoretické minimum
Lineární lomená funkce je každá funkce daná předpisem @b f(x)=\dfrac{ax+b}{cx+d},\quad c\neq 0,\ cb-ad\neq0.@b Výraz @i\,\dfrac{ax+b}{cx+d}\,@i má smysl, když @i\,cx+d\neq 0@i, nulou nelze dělit. Definičním oborem jsou všechna reálná čísla kromě @i\,-\,\dfrac dc@i, tj. @b\mathcal D(f)=\mathbb R\backslash\left\{-\,\dfrac dc\right\}.@b Grafem je hyperbola, kterou získáme transformací souřadnic grafu funkce @b g(x)=\dfrac{1}x .@b Nakresleme graf funkce @i\,f(x)=\dfrac{3x-5}{x-1}@i. Protože nulou nelze dělit, je definiční obor množina všech reálných čísel kromě @i\, 1@i, tj. @i\,\mathcal D(f)=\mathbb R \setminus\{1\}@i. Předpis pro funkci upravíme tak, že provedeme dělení, které je naznačeno zlomkovou čarou, viz dělení mnohočlenů, tj. @i\, \dfrac{3x-5}{x-1} = 3 - \dfrac{2}{x-1}@i. Postupně načrtněme grafy funkcí @i\, f_1 :y= \dfrac{1}{x-1}\, @i a @i\, f_2 :y= \dfrac{-2}{x-1} @i
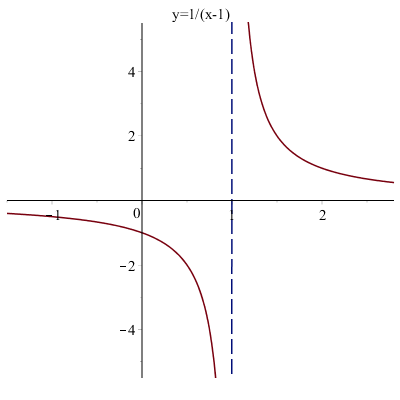
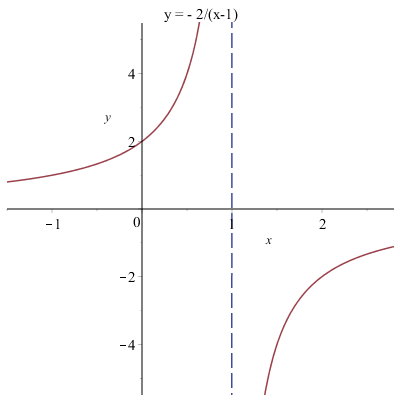
až dostaneme žádaný graf, viz následující obrázek
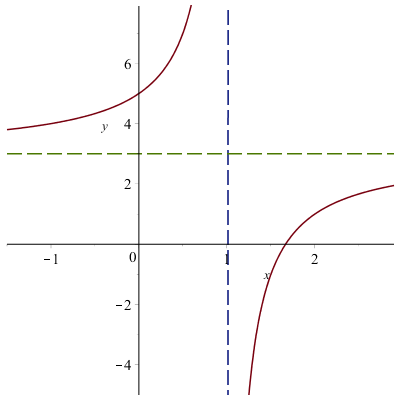
Z grafu snadno vyčteme obor hodnot. Funkční hodnoty leží na svislé ose @i\,y@i. Udělejme kolmý průmět hyperboly na osu @i\,y\,@i a máme obor hodnot @i\,\mathcal H(f)=\mathbb R \setminus\{3\}@i.
Užitečná poznámka: Přímky nakreslené v obrázku čárkovaně se nazývají asymptoty grafu funkce. Přímka @i\,x=1\,@i se nazývá svislá asymptota, přímka @i\,y=3\,@i vodorovná asymptota.
Související
Mnohočleny, definiční obor funkce, graf funkce.
Řešené příklady
- Určete definiční obor funkce @i\, f(x)=\sqrt{\dfrac {1-x}{x+4}}@i.
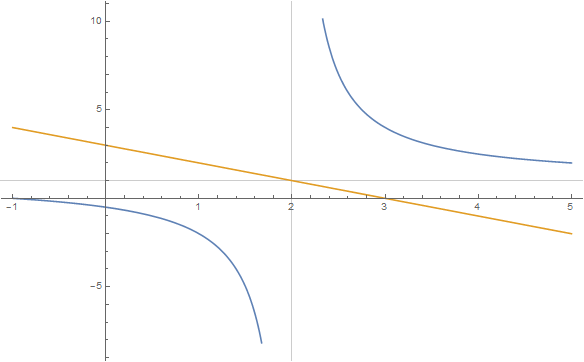
- Graficky řešte nerovnici @i\, \dfrac {2x+3}{1-x}>x@i. Označme funkci na levé straně rovnice písmenkem @i\,f@i, tj. @i\, f(x)= \dfrac {2x+3}{1-x}\,@i a funkci na pravé straně písmenkem @i\,g@i, tj. @i\,g(x)=x @i. Do jednoho obrázku zakreslíme graf funkce @i\,f\,@i a graf funkce @i\,g@i. Grafem funkce @i\,g\,@i je přímka, osa I. a III. kvadrantu. Grafem funkce @i\,f\,@i je hyperbola. Najdeme průsečíky grafu funkce @i\,f\,@i s osu @i\,x@i, tj. dvojice @i\,(x,0)@i. Musíme vyřešit rovnici @i\, \dfrac {2x+3}{1-x}=0@i. Zlomek je roven nule, pokud čitatel se rovná nule, tj. @i\,2x+3=0@i, odtud @i\,x=-\,\dfrac 32.@i Dále najdeme průsečík s osou @i\,y@i, tj. dvojici @i\,(0,f(0)\,)@i. Spočteme funkční hodnotu v nule: @i\,f(0)=3@i. V rovině s kartézskými souřadnicemi zakreslíme body o souřadnicích @i\,(-\,\frac 32,0), (0,3)@i. Dále svislou asymptotu @i\, x=1.@i Vodorovnou asymptotu vyčteme z předpisu, kde čitatel vydělíme jmenovatelem.
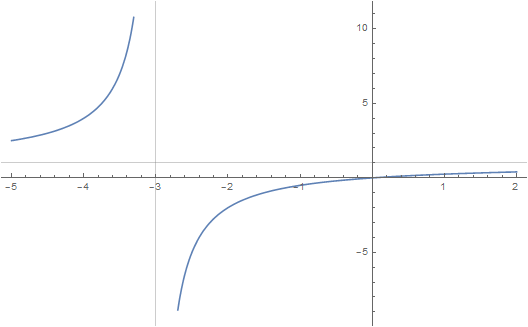
Vypíšeme podmínky, za kterých má funkční předpis smysl. Druhá odmocnina je definovaná pro nezáporná čísla, tj. @i\ \dfrac {1-x}{x+4} \geq 0\,@i a zároveň nelze dělit nulou, tj. @i\, x+4\neq 0@i. Nerovnici můžeme řešit algebraicky, viz nerovnice v součinově podílovém tvaru nebo graficky. Označme si výraz @i\ \dfrac {1-x}{x+4}\,@i jako funkční předpis @i\,g(x)= \dfrac {1-x}{x+4} @i. Grafem funkce @i\,g\,@i je hyperbola. Najdeme průsečíky grafu funkce @i\,g\,@i s osu @i\,x@i, tj. dvojice @i\,(x,0)@i. Musíme vyřešit rovnici @i\, \dfrac {1-x}{x+4}=0@i. Zlomek je roven nule, pokud čitatel se rovná nule, tj. @i\,1-x=0@i, odtud @i\,x=1.@i Dále najdeme průsečík s osou @i\,y@i, tj. dvojici @i\,(0,g(0)\,)@i. Spočteme funkční hodnotu v nule: @i\,g(0)=\dfrac 14@i. V rovině s kartézskými souřadnicemi zakreslíme body o souřadnicích @i\,(1,0), (0,\frac 14)@i. Dále svislou asymptotu @i\, x=-4.@i Vodorovnou asymptotu vyčteme z předpisu, kde čitatel vydělíme jmenovatelem.
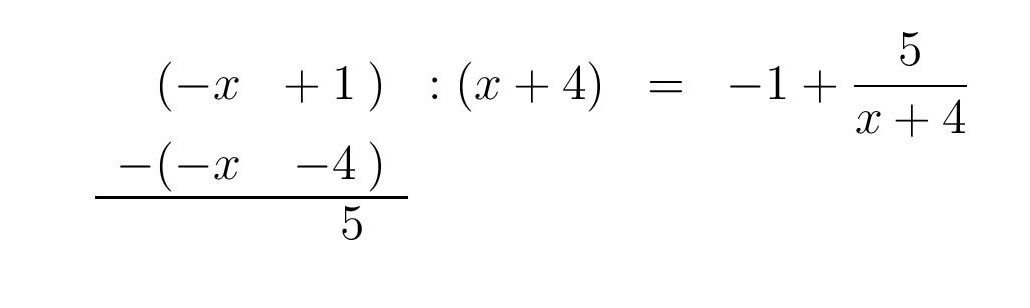
Vodorovná asymptota je @i\, y=-1.@i Body vedeme hyperbolu, viz následující obrázek:
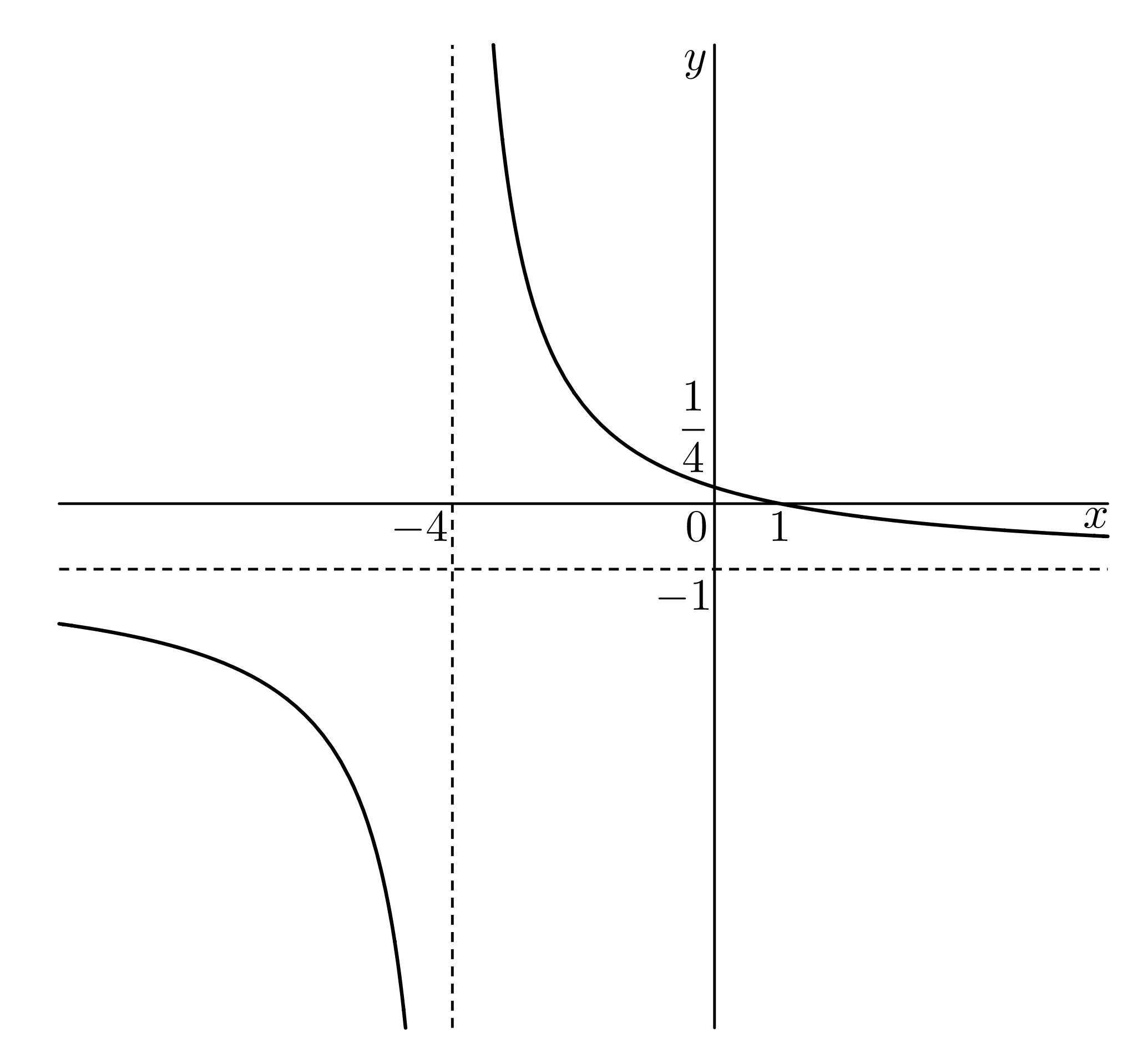
Z obrázku vidíme, že @i\,g(x)\geq 0\,@i pro @i\,x\in (-4,1\rangle.@i Tedy definiční obor je @i\,\mathcal D(f)=(-4, 1\rangle@i.
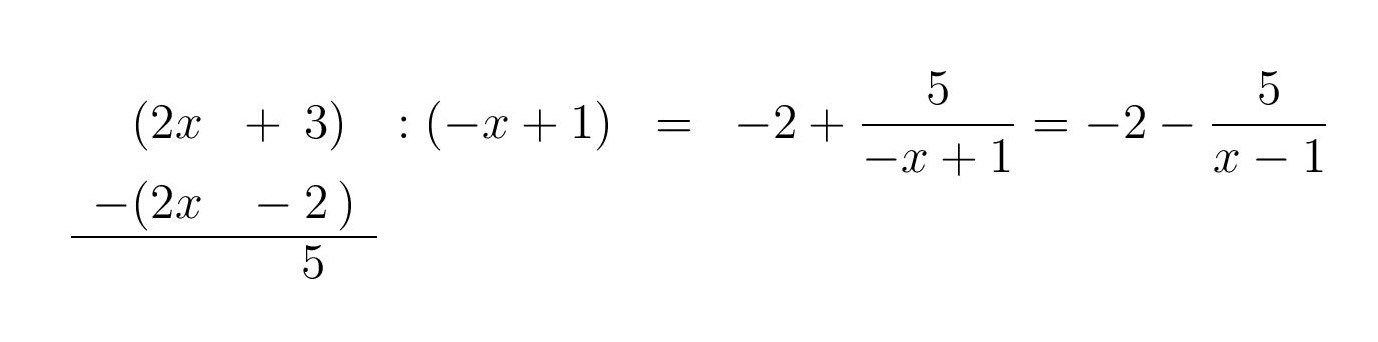
- Vodorovná asymptota je @i\, y=-2.@i Body vedeme hyperbolu, viz následující obrázek:
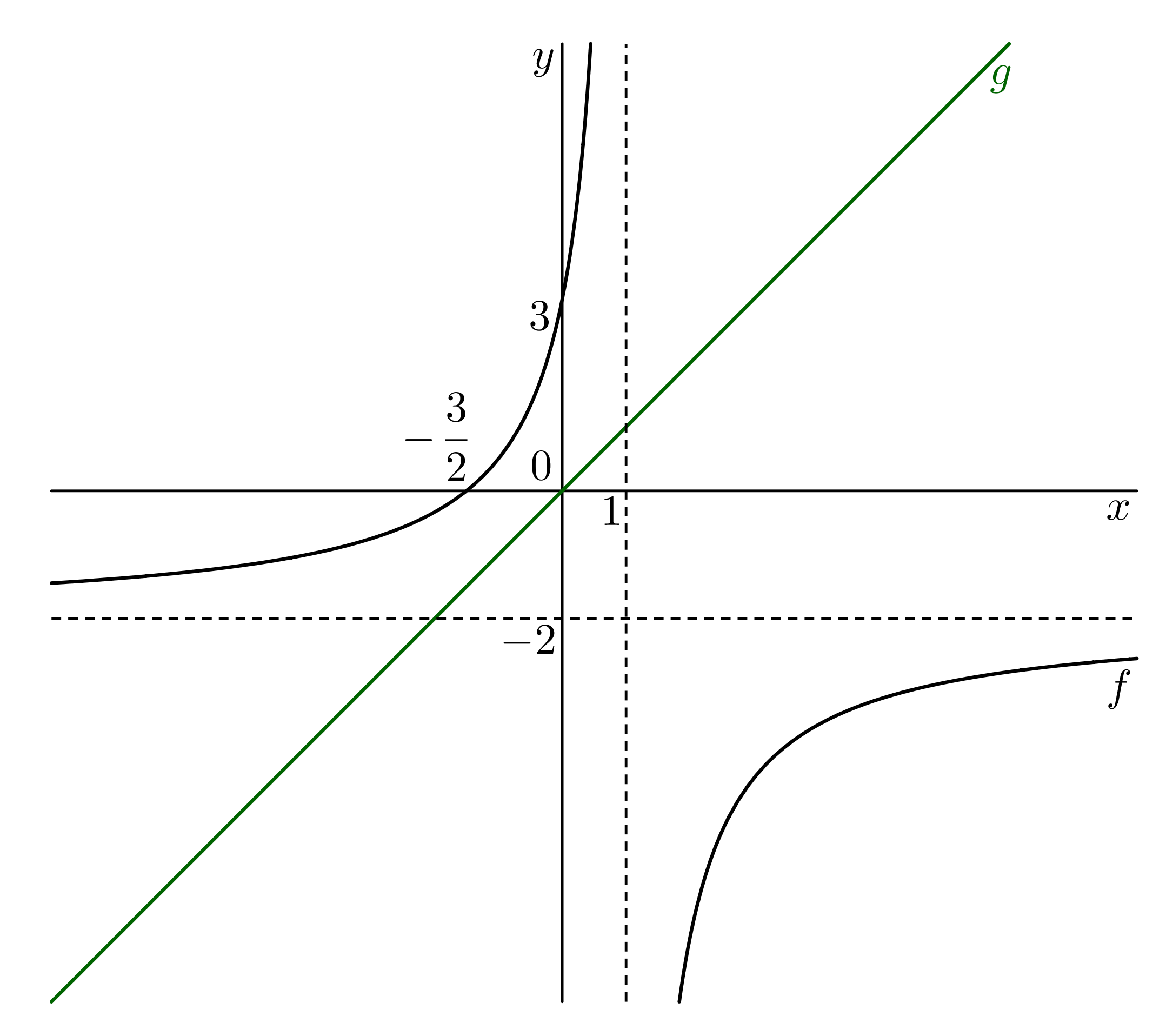
- Řešením dané nerovnice jsou ta @i\,x@i, pro která je graf funkce @i\,f\,@i nad grafem funkce @i\,g@i. Z obrázku snadno vyčteme, že @i\,x\in(-\infty,1)@i.
Pozor, častá chyba: Nerovnici lze řešit algebraicky. Obě strany nerovnice vynásobíme výrazem @i\, (1-x)\,@i a upravíme na kvadratickou nerovnici. @b\begin{array}{rcl} \dfrac{2x+3}{1-x}&>&x / \cdot(1-x)\\[2mm] 2x+3&>&x(1-x)\\[2mm]2x+3&>&x-x^2\\[2mm]x^2+x+3&>& 0\end{array}@b Nejprve hledáme kořeny kvadratické rovnice @b x^2+x+3=0.@b Diskriminat je @i \, D=1-4\cdot3=-11<0 @i. Rovnice nemá kořeny, parabola @i\,y=x^2+x+3\,@i neprotne osu @i\,x@i, celá leží nad sou @i\,x@i, tedy nerovnost je splněna pro každé @i\,x\in\mathbb R @i. Nesmíme však zapomenout, že toto tvrzení platí za předpokladu, že jsme násobili kladným výrazem, tj. @i\,1-x>0@i. Pozor, násobit nulou není ekvivalentní úprava. Zároveň tedy musí platit dvě nerovnosti, že @b x<1\qquad \wedge\qquad x^2+x+3>0.@b Řešením soustavy nerovnic jsou @i\,x\in(-\infty,1)@i. Nesmíme zapomenout na druhou možnost, že @i\,1-x<0@i, násobíme záporným výrazem a je třeba obrátit znaménko, tedy @b x>1\qquad \wedge\qquad x^2+x+3<0.@b Kvadratická nerovnice nemá řešení, parabola @i\,y=x^2+x+3\,@i leží nad osou @i\,x@i. Řešením soustavy nerovnic je prázdná množina. Tedy všechna řešení zadané nerovnice jsou @i\,K=(-\infty,1)@i. Grafické řešení je určitě snažší a hlavně názornější!
Neřešené příklady
- Určete graficky počet kořenů rovnice @i\ \dfrac{x+1}{x-2} = 3-x @i.
- Řešte graficky nerovnici @i\ \dfrac{x}{3+x} \geq 0 @i.