Logo OP VVV

Teoretické minimum

Obecná rovnice

Obecná rovnice přímky v rovině má tvar @b ax +by +c =0\ , @b

kde @i\,a, b, c\, @i jsou nějaká reálná čísla taková, že alespoň jedno z čísel @i\,a\,@i a @i\,b\,@i není rovno @i\,0@i. Body ležící na této přímce jsou právě ty body@i\,X=(x,y)@i, jejichž souřadnice splňují uvedenou rovnost.

Užitečná poznámka: Vektor o souřadnicích @i\, (a,b)\,@i je normálovým vektorem přímky, tj. vektorem, který je kolmý na danou přímku.

Užitečná poznámka:  Vynásobíme-li rovnici přímky nějakým nenulovým číslem (ekvivalentní úprava), pak dostaneme rovnici téže přímky, protože řešením ekvivalentní rovnice jsou souřadnice stále stejných bodů v rovině. Tedy např. @i\ 3x+2y-6=0\ @i a @i\ -x -\frac{2}{3}y + 2= 0 \ @i jsou rovnice stejné přímky.

Všimněte si, že:

  1. Přímka daná rovnicí @i\ ax + c=0@i, tj. @i\,b=0@i, je rovnoběžná s osou @i\,y@i.
  2. Přímka daná rovnicí @i\ by + c=0@i, tj. @i\,a=0@i, je rovnoběžná s osou @i\,x@i.
  3. Přímka daná rovnicí @i\ ax +by + c=0@i, kde @i\,a\neq 0\,@i a @i\,b\neq 0@i, není rovnoběžná ani s osou @i\,x\,@i ani s osou @i\,y@i.

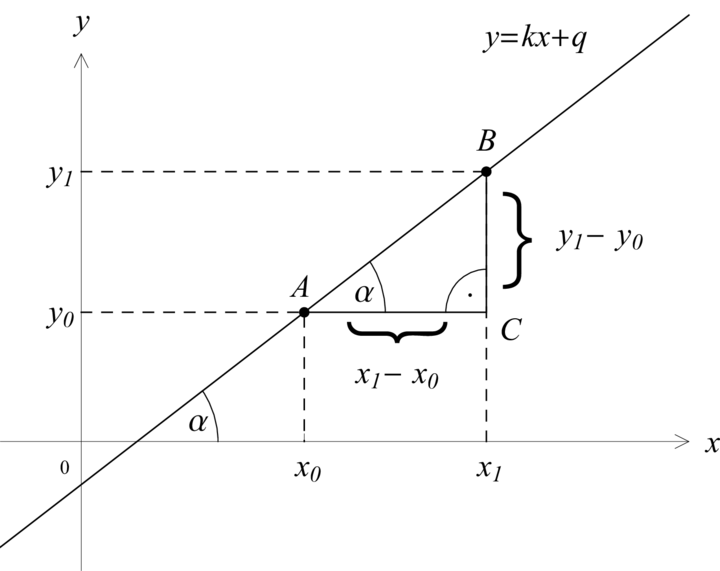
V rovnici přímky v obecném tvaru @i\,ax +by +c=0@i, nejsou koeficienty @i\,a, b, c\, @i určeny jednoznačně. Může být výhodné volit koeficient u proměnné @i\,y\,@i rovný jedné a psát rovnici přímky ve tvaru @b y=kx +q,@b který nazýváme směrnicový tvar rovnice přímky  a číslo@i\,k\,@i směrnicí přímky @i\,p@i. Zdůrazněme, že to lze udělat pouze v případě, že přímka není rovnoběžná s osou @i\,y@i, tedy v obecné rovnici je koeficient @i\,b\,@i různý od @i\,0@i.

Geometrický význam čísel @i\,k\,@i a @i\,q@i
Pro směrnici @ik@i přímky @ip@i platí @ik={\mathrm{tg}}\alpha@i, kde @i\alpha@i je úhel, který svírá přímka @ip@i s kladným směrem osy @ix@i.
Číslo @iq@i je pak @iy@i-ová souřadnice průsečíku přímky @ip@i s osou @iy@i.

To nahlédneme následovně: Uvažujme nejprve @ik>0@i. Zvolme dva různé body @iA=({x_0},{y_0})@i a @iB=({x_1},{y_1})@i, které leží na přímce @ip@i s rovnicí @iy=kx +q@i.(Přímka @ip@i není rovnoběžná s osou @iy@i, tedy @i{x_0}\neq {x_1}@i.) Pak @i{y_0}=k{x_0} +q@i a také @i{y_1}=k{x_1} +q@i. Odečtením těchto dvou rovnic dostaneme @i{y_1}-{y_0}= k({x_1}-{x_0})@i, a tedy @ik= {\displaystyle \frac{{y_1}-{y_0}}{{x_1}-{x_0}}}@i. Jelikož v pravoúhlém trojúhelníku @iABC@i je tangens úhlu @i\alpha@i roven poměru velikosti protilehlé odvěsny ku velikosti přilehlé odvěsny, dostáváme

@i {\mathrm{tg}}\alpha = \frac{{y_1}-{y_0}}{{x_1}-{x_0}} =k\ . @i

Celá situace je nakreslena na následujícím obrázku. Pro @ik< 0@i lze postupovat obdobně.
Dosazením @ix=0@i do rovnice přímky zřejmě dostaneme @iy=q@i, tedy bod @i(0,q)@i je bodem přímky @ip@i. Je to tedy její průsečík s osou @iy@i.


V předchozím jsme vlastně ukázali následující:

Prochází-li přímka body @iA=({x_0},{y_0})@i a @iB=({x_1},{y_1})@i, @i{x_0}\neq {x_1}@i, je její směrnice @ik@i dána vztahem

@i k= \dfrac{{y_1}-{y_0}}{{x_1}-{x_0}}\ . @i

Znaménko směrnice přímky určuje, zda je funkce @iy=kx+q@i rostoucí či klesající, tj. zda se zvětšujícím se @ix@i se hodnoty @iy@i zvětšují či zmenšují. Platí:

  • Je-li @ik>0@i, je @i0< \alpha < \pi /2@i a funkce @iy=kx+q@i je rostoucí.
  • Je-li @ik<0@i, je @i\pi /2 < \alpha < \pi @i a funkce @iy=kx+q@i je klesající.
  • Je-li @ik=0@i, je přímka @ip@i rovnoběžná s osou @ix@i a @iy=q@i je konstantní funkce.
Poznámka: Je-li dokonce @ia\neq 0,@i @ib\neq 0@i  a @i c\neq0,@i protíná přímka @iax+by+c=0@i osový kříž ve dvou bodech. Jsou - li v tomto případě @i P_x = (p,0)@i a @i P_y= (0,q)@i průsečíky s osami, pak lze rovnici přímky psát v úsekovém tvaru:
@i \dfrac{x}{p} + \dfrac{y}{q}=1.@i

Parametrické vyjádření

Jak víme, přímka je určena dvěma svými body. Podobně může být přímka také určena jedním svým bodem a vektorem, který udává její směr. To si podrobně vysvětlíme v následujícím odstavci. Vektorem @i\vec{u}@i (v rovině) rozumíme uspořádanou dvojici reálných čísel, tj. @i\vec{u}= ({u_1},{u_2})@i, a znázorňujeme jej jako orientovanou úsečku, která vede z počátku @iP=(0,0)@i do bodu o souřadnicích @i({u_1},{u_2})@i, nebo z nějakého bodu @iA=({x_0},{y_0})@i do bodu @iB=({x_0}+{u_1},{y_0}+{u_2})@i.


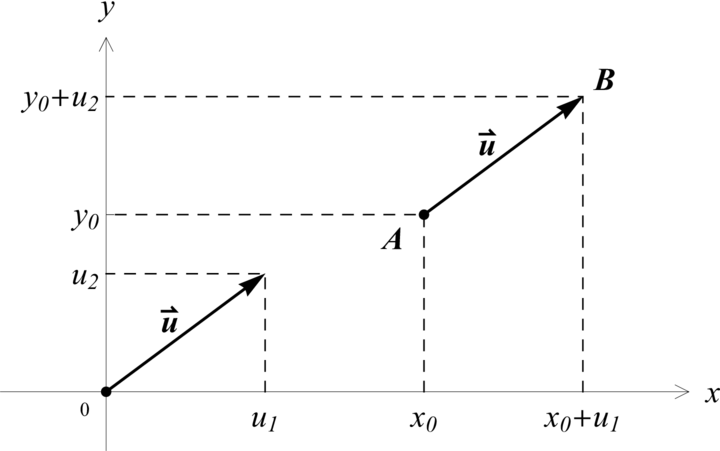
Zvolení bodu @iA@i, ze kterého vektor @i\vec{u}@i nakreslíme, nazýváme umístěním vektoru @i\vec{u}@i. Bod @iA@i pak nazýváme počátečním bodem vektoru @i\vec{u}@i a bod @iB@i koncovým bodem vektoru @i\vec{u}@i. Píšeme též @i\vec{u}=\overrightarrow{AB}@i .

Body přímky @ip@i, která prochází bodem @iA=({a_1},{a_2})@i a má směr (přesněji má směrový vektor) @i\vec{u}= ({u_1},{u_2})@i, dostáváme tak, že do bodu @iA@i umísťujeme různé násobky vektoru @i\vec{u}@i . Koncové body takto umístěných vektorů jsou pak body přímky @ip@i, viz následující obrázek.



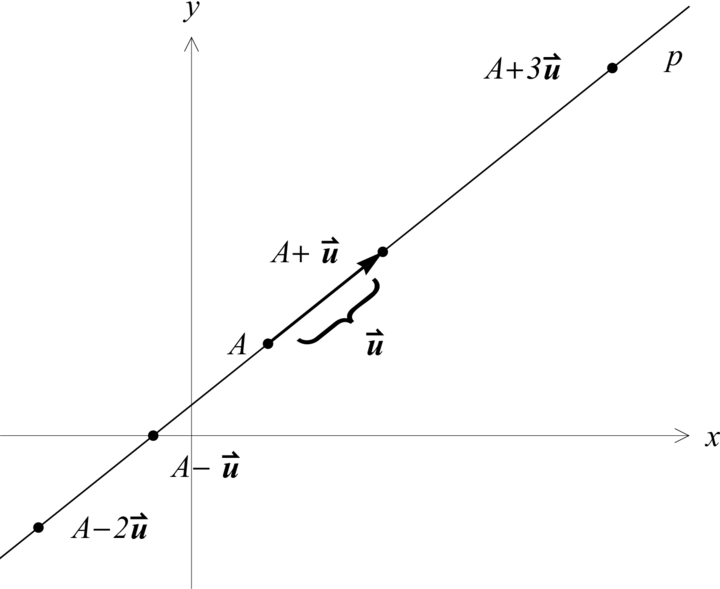
Uvědomte si a ukažte na obrázku, které body na přímce @ip@i dostanete, když k bodu @iA@i přičtete např. @i\vec{u}@i, @i3\vec{u}@i, @i-\vec{u}@i, @i-2\vec{u}@i, @i0 \cdot \vec{u}@i. Dále si uvědomte, že přičtením všech reálných násobků vektoru @i\vec{u}@i k bodu @iA@i dostaneme právě všechny body přímky @ip@i.

To se formálně zapíše takto:

@i X=A+t\vec{u},\ t\in \mathbb{R}, @i

což rozepsáno do souřadnic dává

@i \begin{array}{rcl} x & = & {a_1} + t {u_1} \\ y & = & {a_2} + t {u_2} \end{array}\ , \ \ t \in \mathbb{R}\ . @i

Tyto rovnice nazýváme parametrickými rovnicemi přímky @ip@i procházející bodem @iA@i se směrovým vektorem @i\vec{u}@i. Pro různé volby parametru @it \in \mathbb{R}@i pak dostáváme souřadnice různých bodů přímky @ip@i.

Uvědomte si, že směrový vektor @i\vec{u}=({u_1},{u_2})@i přímky @ip@i je určen až na nenulový násobek, tj. je-li @i\alpha \in \mathbb{R}@i, @i\alpha \neq 0@i, pak i vektor @i\alpha \vec{u} =(\alpha {u_1},\alpha {u_2})@i je směrovým vektorem přímky @ip@i. Jsou-li zadané dva (různé) body @iA=({a_1},{a_2})@i a @iB=({b_1},{b_2})@i přímky @ip@i, pak za směrový vektor přímky @ip@i můžeme volit vektor @i\overrightarrow{AB}= B-A = ({b_1}-{a_1},{b_2}-{a_2})@i.

 

Poznámka:   Směrový vektor a normálový vektor jsou na sebe kolmé. V rovině zkonstruujeme vektor kolmý k danému vektoru snadno. Je-li totiž @i \vec{u}=(a,b)@i, pak je vektor @i\vec{v}=(b, -a)@i kolmý na @i \vec{u} @i.

Řešené příklady

  1. Mějme přímku @ip@i danou následující rovnicí @i3x+2y-6=0@i. Určeme několik bodů, které leží na @ip@i a několik bodů, které neleží na @ip@i.

    2. Na přímce @ip@i leží například body @i(0,3)(2,0),(-1, \frac 92)@i a jiné. Jejich souřadnice vyhovují rovnici @i3x+2y-6=0@i. Na přímce @ip@i neleží například body @i(0,0)(2,-2),(-1,5)@i a jiné. Jejich souřadnice nevyhovují rovnici @i3x+2y-6=0@i.
  2. Určeme rovnici přímky@iAB@i procházející body @iA=(3,2)@i a @iB=(4,-1)@i.

    3. I. způsob řešení  Na první pohled vidíme, že přímka @iAB@i s osou @iy@i rovnoběžná není, protože @ix@i-ové souřadnice bodů @iA@i a @iB@i jsou různé. Můžeme tedy její rovnici hledat ve směrnicovém tvaru @iy=kx +q@i. Dosadíme-li do této rovnice souřadnice bodů @iA@i a @iB@i, dostaneme dvě rovnice pro neznámé @ik@i a @iq@i, totiž rovnice

    @i 2=3k+q \hspace{1cm} {\rm a} \hspace{1cm} -1=4k+q \ . @i

    Odtud dostáváme @ik=-3@i a @iq=11@i a rovnice hledané přímky je @iy=-3x +11@i. O správnosti výsledku se můžeme snadno přesvědčit dosazením souřadnic bodů @iA@i a @iB@i do nalezené rovnice. Musíme dostat platné rovnosti. 

    II. způsob řešení Odečtením souřadnic bodů dostaneme směrový vektor přímky @i \vec{u} = B-A = (1,-3)  @i. Normálový vektor přímky dostaneme v rovině snadno prohozením souřadnic a jednoho znaménka @i \vec{n} = (3,1).@i Obecná rovnice má tedy tvar @i 3 x + 1y +c=  0.@i Konstantu @i c @i určíme tak, aby přímka procházela zadanými body @i3 \cdot 3 + 1 \cdot 2 + c =0,@i odkud @i c= -11@i a dostáváme hledanou rovnici přímky ve tvaru @i 3x+ y - 11 =0 .@i
  3. Napišme rovnici přímky @ip@i, která prochází bodem @iA=(1,2)@i a je kolmá k přímce @iq@i procházející body @iB=(-3,0)@i a @iC=(1,-2)@i.

    4. Vektor @i \vec{u} = C-B = (4,-2)@i je směrovým vektorem přímky @iq@i. Jako normálový vektor přímky @ip@i lze volit jeho libolný nenulový násobek např. @i \vec{n} = (2,-1).@i Proto lze psát rovnici přímky @i p @i ve tvaru @i 2x -y + c =0 @i. Dosazením souřadnic bodu @i A @i dostaneme @ic= 0.@i @b p:\:2x =y.@b
  4. Napišme směrnicový tvar rovnice přímky @ip@i, která prochází body @iP=(0,2)@i a @iQ=(-3,0).@i

    5. S využitím poznámky o úsekovém tvaru dostáváme okamžitě rovnici ve tvaru @i\dfrac{x}{-3} + \dfrac{y}{2} = 1.@i Směrnicový tvar rovnice je tedy @b y = 2+ \dfrac{2}{3}x.@b
  5. Napišme nějaké parametrické vyjádření přímky @i p:\:3x + y = 4.@i

    6. Zavedeme parametr (např.) @i x=t .@i Druhou proměnnou dopočteme @i y=4-3t. @i 
    @i \begin{array}{rcl} x & = &t \\ y & = & 4-3t \end{array}\ , \ \ t \in \mathbb{R}\ . @i

Související

Parametricky zadané křivky.

Neřešené příklady

  1. Určete rovnici přímky @iAB@i procházející body @iA=(4,-3)@i a @iB=(12,1)@i. Napište její úsekový tvar a určete průsečíky přímky se souřadnými osami.
  2. Napište rovnici přímky @ip@i, která prochází bodem @iA=(2,3)@i a je kolmá k přímce @iq@i procházející body @iB=(1,-3)@i a @iC=(0,2)@i.
  3. Určete průsečík @iP@i přímek @ip@i a @iq@i, jsou-li přímky @ip@i, @iq@i zadány obecnými rovnicemi @i3x+4y+5=0@i a @i-x+y-4=0@i.
  4. Napište obecnou rovnici přímky s parametrickým vyjádřením @i\:\: p:\: \begin{array}{rcl} x & = &1-t \\ y & = & 3+2t \end{array}\ , \ \ t \in \mathbb{R}\ . @i
  5. Určete vzájemnou polohu přímek @i p @i a @iq@i, kde @ip: -x+3y=2,@i a @i q:\begin{array}{rcl} x & = &2+6t \\ y & = & 1+2t \end{array}\ , \ \ t \in \mathbb{R} .@i

Licence CC BY

Naposledy změněno: středa, 8. června 2022, 14.09