Goniometrické funkce, rovnice a nerovnice
Goniometrické funkce, rovnice a nerovnice

Teoretické minimum
Uvažme v kartézské souřadnicové soustavě kružnici @i\,K\,@i o poloměru @i\,1\,@i se středem v počátku a na ní bod @i\,A=(1,0)@i. Zvolme @i\,x\in\mathbb R@i. Pro @i\,x\geq 0\,@i posunujeme bod @i\,A\,@i po kružnici @i\,K\,@i v kladném směru (tj. proti směru hodinových ručiček) tak, že urazí dráhu @i\,x@i. Bod, do kterého bod @i\,A\,@i přejde, označme @i\,X@i. Pak @i\,x@i-ová souřadnice bodu @i\,X\,@i je právě hodnota @i\,\cos x\,@i a @i\,y@i-ová souřadnice bodu @i\,X\,@i je právě hodnota @i\,\sin x@i, tedy @i\,X=(\cos x, \sin x)@i, viz následující obrázek:
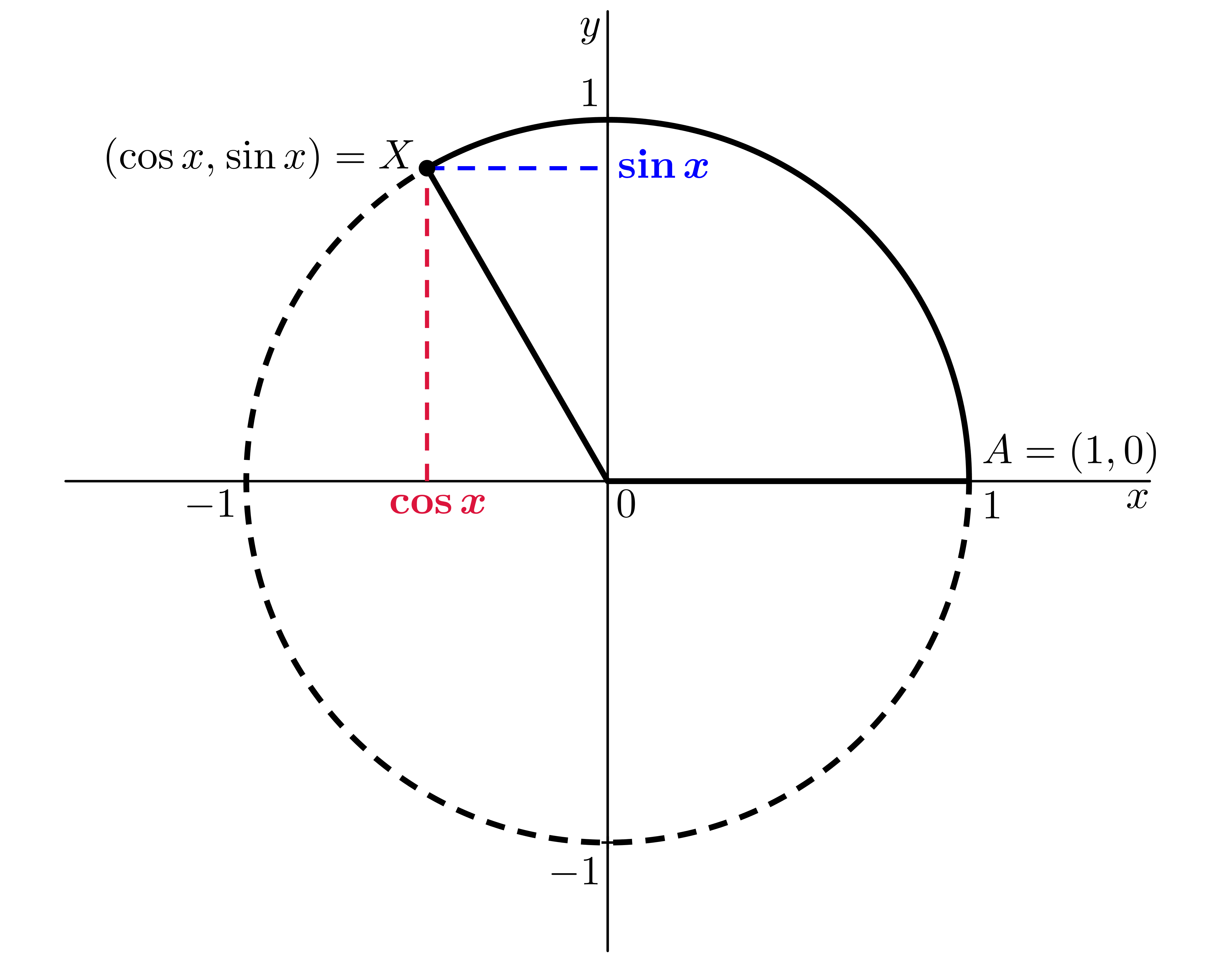
Pro @i\,x<0\,@i posunujeme bod @i\,A\,@i po kružnici @i\,K\,@i v záporném směru (tj. po směru hodinových ručiček) tak, že urazí dráhu @i\,-x=|x|@i. Opět označme bod, do kterého bod @i\,A\,@i takto přejde, jako bod @i\,X@i. Pak stejně @i\,x@i-ová souřadnice bodu @i\,X\,@i je hodnota @i\,\cos x\,@i a @i\,y@i-ová souřadnice bodu @i\,X\,@i je hodnota @i\,\sin x@i.
Ke každému reálnému číslu @i\,x\,@i existuje právě jedno reálné číslo @i\,\cos x\,@i a právě jedno reálné číslo @i\,\sin x@i. Hodnoty @i\,\cos x,\ \sin x\,@i jsou funkční hodnoty goniometrických funkcí kosinus @i\,x\,@i a sinus @i\,x\,@i proměnné @i\,x@i, které zapisujeme: @b f(x)=\sin x,\qquad \qquad g(x)=\cos x.@b Funkce @i\,f\,@i a @i\,g\,@i jsou definované pro každé reálné číslo, tj. @b\mathcal D(f)=\mathcal D(g)=\mathbb R.@b Funkční hodnoty jsou větší rovny @i\,-1\,@i a menší rovny @i\,1@i, tj. @b\mathcal H(f)=\mathcal H(g)=\langle -1,1 \rangle.@b Jejich grafy jsou nakresleny na následujících obrázcích:
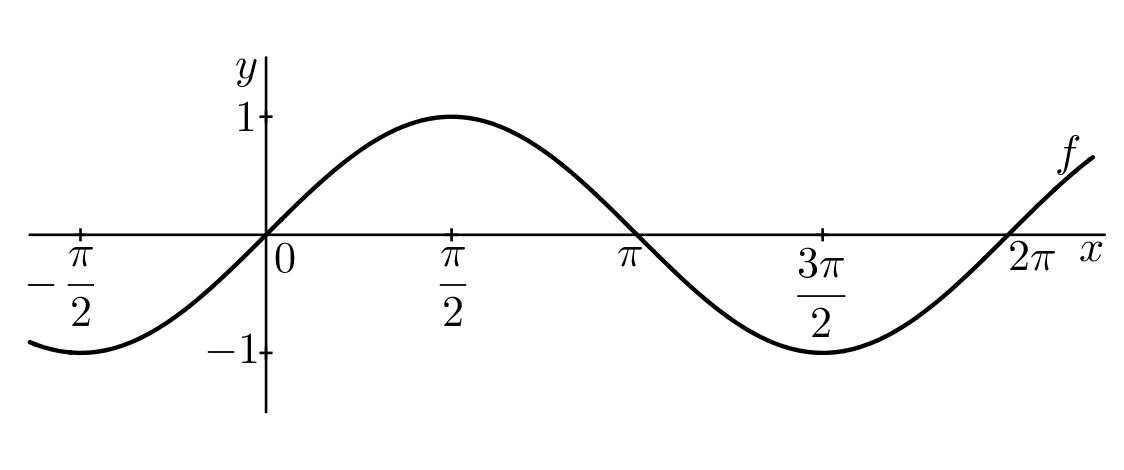
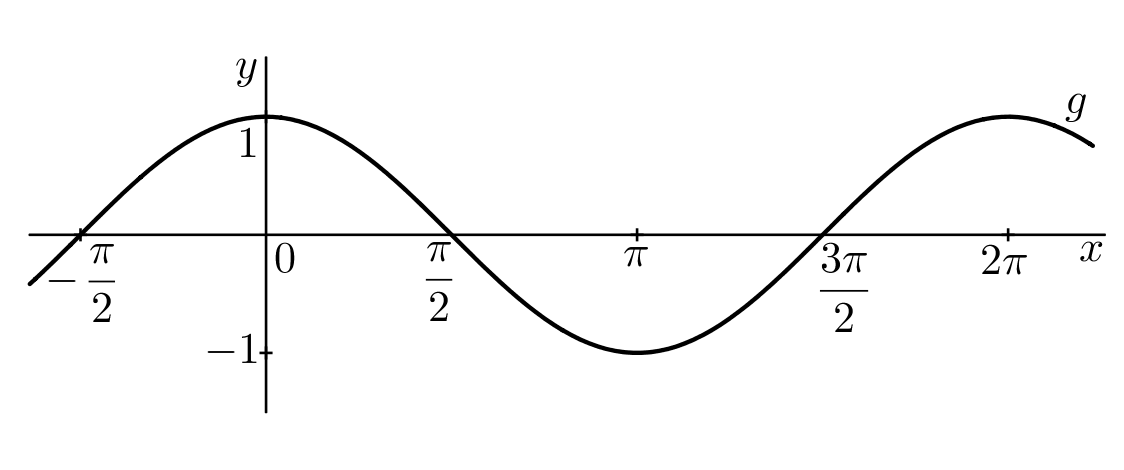
1. @b\sin(x+2\pi)=\sin x,\qquad\qquad \cos(x+2\pi)=\cos x.@b Říkáme, že funkce @i\,f\,@i a @i\,g\,@i mají periodu @i\,2\pi@i.
2. @b\sin(-x)=-\sin x,\qquad\qquad \cos(-x)=\cos x.@b Říkáme, že funkce @i\,f(x)=\sin x\,@i je funkce lichá, její graf je symetrický podle počátku. Funkce @i\,g(x)=\cos x\,@i je funkce sudá, její graf je symetrický podle osy @i\,y@i.
3. Z Pythagorovy věty dostáváme @b\sin^2 x+\cos^2 x=1.@b
4. S trochu větším úsilím je možno odvodit i další vzorce: @b\sin 2x=2\sin x \cos x,\qquad\qquad \cos 2x=\cos^2 x - \sin^2 x.@b
Rovněž je důležité znát nazpaměť hodnoty funkcí pro konkrétní hodnoty proměnné @i\,x\,@i (z I. kvadrantu) uvedené v následující tabulce:
@b \begin{array}{|c|c|c|c|c|c|c|c|}\hline x& &0 &\dfrac \pi 6&\dfrac \pi 4&\dfrac \pi 3&\dfrac \pi 2\\ \hline \hline \sin x && 0& \dfrac 12 & \dfrac {\sqrt 2}2&\dfrac {\sqrt 3}2&1 \\ \hline\cos x &&
1& \dfrac {\sqrt 3}2 & \dfrac {\sqrt 2}2&\dfrac {1}2&0\\\hline \end{array} @b
Další goniometrické funkce jsou tangens a kotangens, které zavádíme pomocí následujících vztahů: @b\mathrm{tg}\, x=\dfrac{\sin x}{\cos x},\qquad\qquad \mathrm{cotg}\, x=\dfrac{\cos x}{\sin x}.@b
Odtud vidíme, že funkce tangens je definována pro ty hodnoty @i\, x\in\mathbb R@i, kdy @i\,\cos x\neq 0@i, tedy pro @i\,x\neq\frac \pi 2+k\pi=(1+2k)\frac \pi 2,\ k\in\mathbb Z@i. Funkce kotangens je definována pro ty hodnoty @i\, x\in\mathbb R@i, kdy @i\,\sin x\neq 0@i, tedy pro @i\,x\neq k\pi,\ k\in\mathbb Z@i. Tj. jejich definiční obory jsou @b\mathcal D(\mathrm{tg})=\mathbb R\setminus\bigcup\limits_{k\in\mathbb Z}\Bigl \{(2k+1)\frac\pi 2\Bigr \},\qquad\qquad \mathcal D(\mathrm{cotg})=\mathbb R\setminus\bigcup\limits_{k\in\mathbb Z}\bigl \{k\pi\bigr \}.@b Grafy funkcí tangens a kotangens jsou nakresleny na následujících obrázcích:
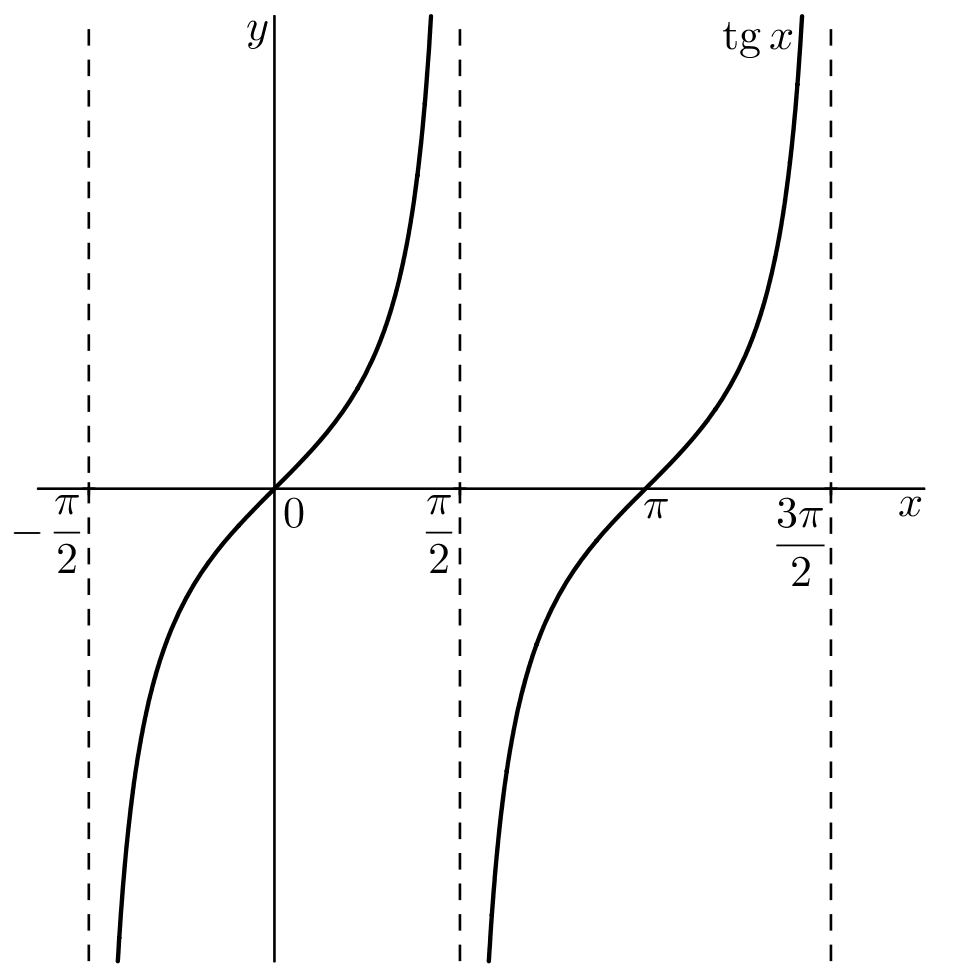
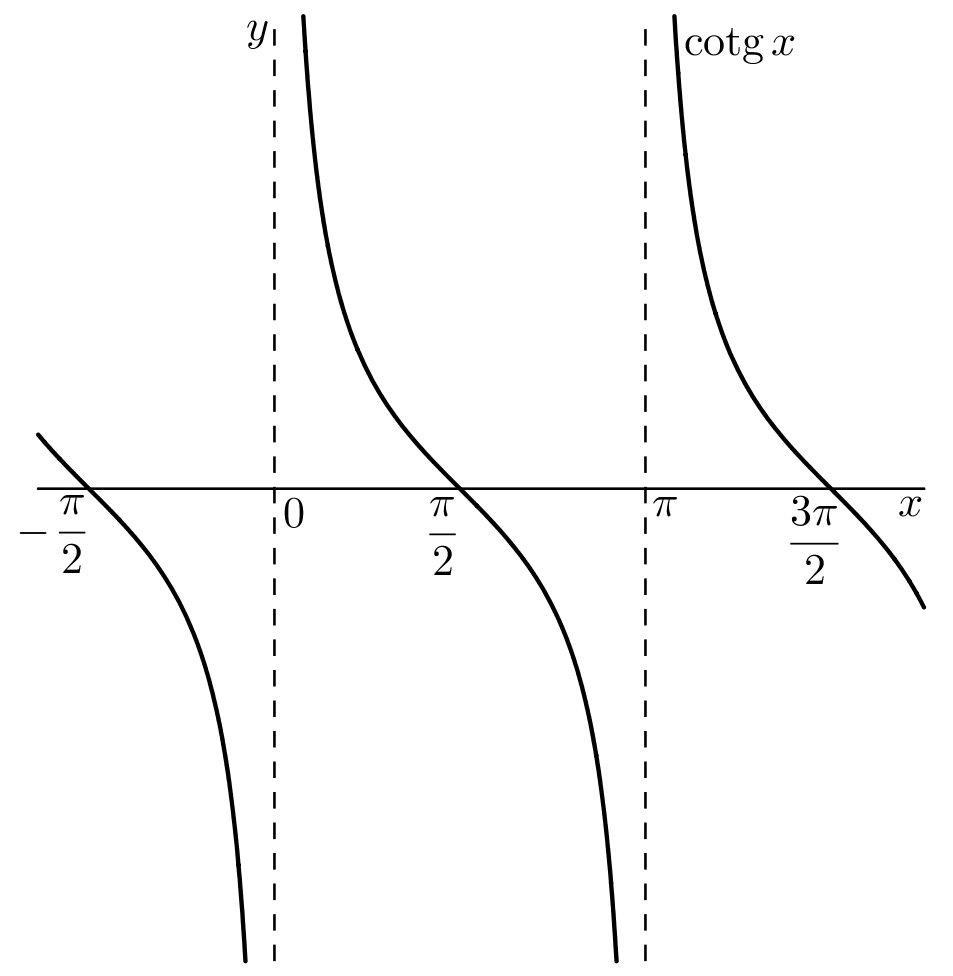
Z obrázků vidíme, že obor hodnot funkce tangens i kotangens jsou všechna reálná čísla, tj. @b\mathcal H(\mathrm{tg})=\mathcal H(\mathrm{cotg})=\mathbb{R}.@b
Z tabulky hodnot funkcí sinus a kosinus pro konkrétní hodnoty proměnné @i\,x\,@i (z I. kvadrantu) snadno odvodíme následující tabulku
@b \begin{array}{|c|c|c|c|c|c|c|c|}\hline x& &0 &\dfrac \pi 6&\dfrac \pi 4&\dfrac \pi 3&\dfrac \pi 2\\ \hline \hline \mathrm{tg}\, x && 0& \dfrac {\sqrt 3}3 & 1&\sqrt 3 &-\\ \hline\mathrm{cotg}\, x
&& -& \sqrt 3 & 1&\dfrac {\sqrt 3}3& 0\\\hline \end{array} @b
kterou je třeba též znát na zpaměť.
Užitečná poznámka: Funkce @i\,f(x)=\mathrm{tg} \,x\,@i a @i\,g(x)=\mathrm{cotg} \,x\,@i mají periodu @i\,\pi@i a jsou liché. Tedy platí následující vztahy: @b\mathrm{tg}(x+\pi)=\mathrm{tg}\, x,\qquad\qquad \mathrm{cotg}(x+\pi)=\mathrm{cotg}\, x,@b @b\mathrm{tg}(-x)=-\mathrm{tg}\, x,\qquad\qquad \mathrm{cotg}(-x)=-\mathrm{cotg}\, x.@b
Goniometrickou rovnicí nazýváme rovnici, která obsahuje neznámou v argumentu některé z goniometrických funkcí. Řešit takovou rovnici znamená najít všechny orientované úhly, které dané rovnici vyhovují. Vzhledem k periodičnosti goniometrických funkcí mají goniometrické rovnice zpravidla nekonečně mnoho řešení, pokud nespecifikujeme interval, v němž hledáme konkrétní řešení.
Související
Definiční obor funkce, graf funkce.
Řešené příklady
- Vyčíslete hodnoty @i\ \sin \frac 56\pi,\ \cos \frac 56\pi,\ \mathrm{tg} \frac 56\pi,\ \mathrm{cotg} \frac 56\pi@i.
- Nakreslete graf funkce @i\ f(x)=3\cos 2x@i.
- Určete periodu funkce @i\ f(x) = \sin \bigl(3x+\frac{\pi}{4}\bigr)@i.
- Vypočtěte průsečíky grafu funkce @i\ f(x)=\mathrm{cotg}\Bigl(2x+\dfrac \pi2\Bigr)\,@i s osou @i\,x@i.
- Určete, kdy má výraz @i \ \Bigl(\dfrac{\sin(2x)}{\cos^2 x}+2\mathrm{tg}^3\,x\Bigr)\cdot \sin\Bigl(\frac{3\pi}{4}\Bigr)\,@i smysl a zjednodušte ho.
- Určete definiční obor funkce @i \ f(x)=\dfrac{\mathrm{tg}\Bigl(2x+\dfrac{\pi}{3}\Bigr)}{2-\sin x }@i.
- Řešte v oboru reálných čísel rovnici @i\ \cos x=-\,\dfrac 12@i.
- Řešte v oboru reálných čísel nerovnici @i\ \mathrm{tg}\left(x+\dfrac \pi 3 \right)>\dfrac{\sqrt 3}3@i.
Protože úhel @i\,x=\frac 56\pi\,@i je ze II. kvadrantu, musíme najít odpovídající úhel z I. kvadrantu. Platí @i\,\frac 56\pi=\pi-\frac \pi 6@i. Z jednotkové kružnice vyčteme
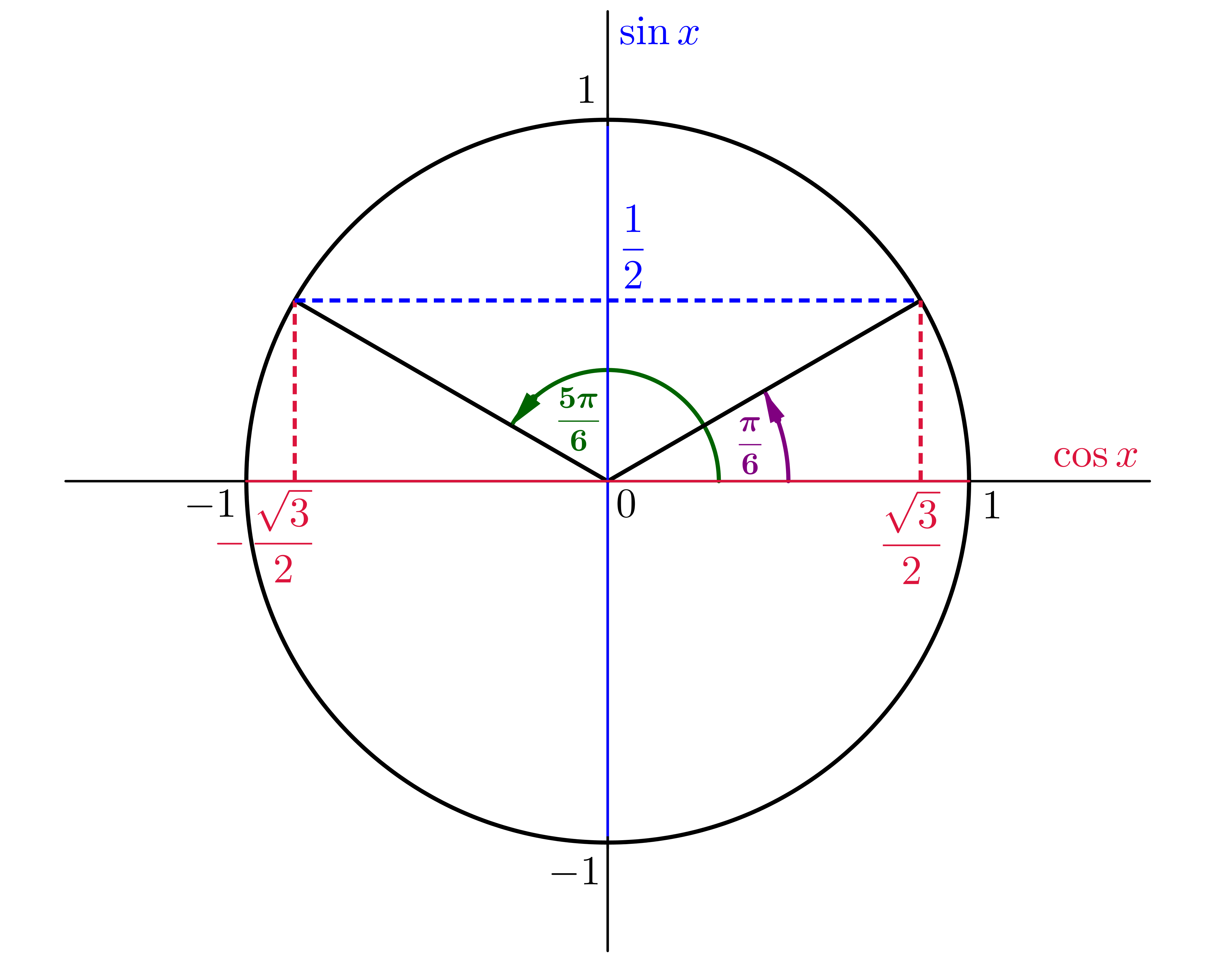
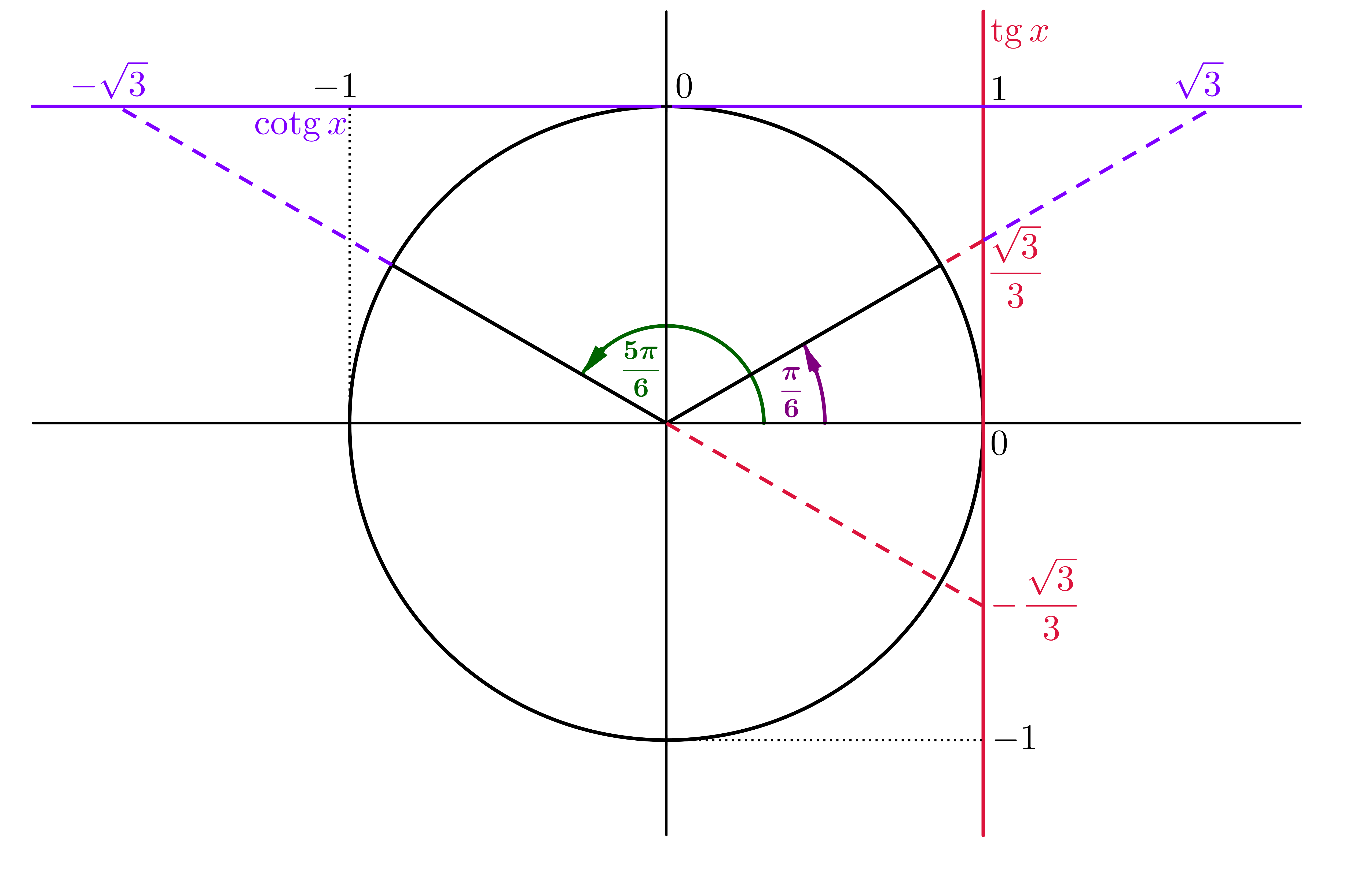
@b\sin \frac 56\pi=\sin\frac \pi 6=\frac 12.@b Poslední hodnotu známe nazpaměť. Dále @b\cos \frac 56\pi=-\,\cos\frac \pi 6=- \,\frac {\sqrt 3}2,@b @b\mathrm{tg} \,\frac 56\pi=-\,\mathrm{tg}\,\frac \pi 6=-\, \frac{\sqrt 3}3,@b @b\mathrm{cotg} \,\frac 56\pi=-\,\mathrm{cotg}\,\frac \pi 6=-\ \sqrt 3.@b
Perioda funkce kosinus je @i\,2\pi@i. Funkce @i\,g(x)=\cos 2x\,@i má periodu poloviční, tedy @i\,p=\pi@i. Obor hodnot funce @i\,f\,@i se ztrojnásobí, tedy @i\,\mathcal H(f)=\langle -3,3\rangle@i.
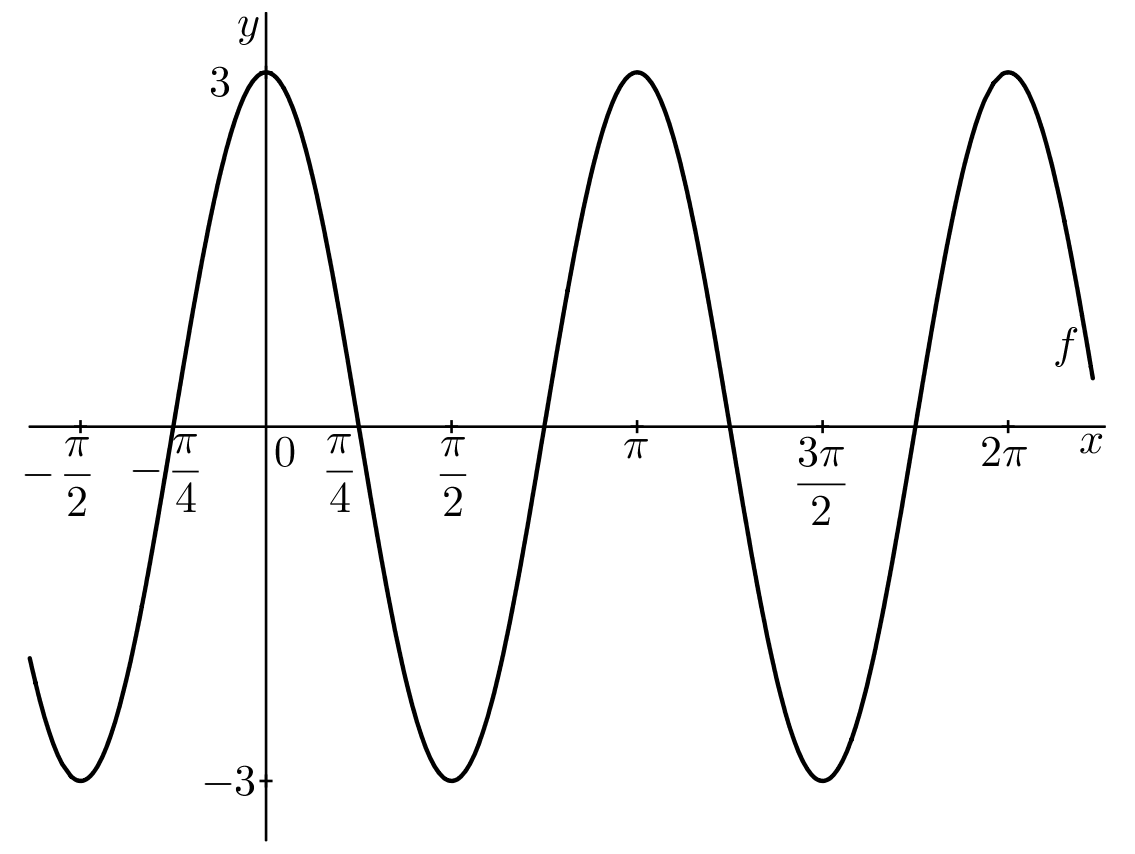
Užitečná poznámka: Nechť @i\,f\,@i je periodická funkce s periodou @i\,p\,@i, pak funkce @i\,f(ax), a> 0\,@i má periodu @i\,\dfrac pa@i.
Funkce sinus má periodu @i2\pi.@i Proto @b f(x) = \sin \bigl(3x+\frac{\pi}{4}\bigr) = \sin \bigl(3x +\frac{\pi}{4} + 2\pi \bigr) = \sin \bigl(3x +\frac{\pi}{4} + 3\cdot\frac{2}{3}\pi \bigr) = \sin
\Bigl(3 \bigl(x +\frac{2}{3}\pi \bigr) +\frac{\pi}{4} \bigr) = f\bigl(x +\frac{2}{3}\pi \bigr). @b Funkce @if@i je tedy @i\frac23\pi@i-periodická.
Užitečná poznámka: Budeme-li kreslit graf funkce @i\,f(x)=\sin\bigl(3x+\frac \pi 4\bigr)@i, je třeba v argumentu funkce sinus vytknout @i\,3@i. Tedy @i\,f(x)=\sin\bigl(3 (x+\frac \pi {12})\bigr)@i. Graf funkce sinus posuneme o @i\,\frac \pi{12}\,@i jednotek ve směru osy @i\,x\,@i doleva a poté periodu třikrát zmenšíme, tj. @i\,p=\frac {2\pi}3@i.
Průsečík grafu funkce @i\,f\,@i s osou @i\,x\,@i je bod o souřadnicí @i\,(x,0)@i. Tedy musíme vyřešit rovnici @b\mathrm{cotg}\Bigl(2x+\frac \pi2\Bigr)=0. @b Funkce kotangens nabývá nulové hodnoty pro @i\,x=\dfrac \pi2+k\pi,\ k\in\mathbb Z@i. Proto @b
2x+\frac \pi 2=\frac\pi2+k\pi. @b Odtud @i\, x=k\cdot\dfrac \pi2@i. Funkce @i\,f\,@i má nekonečně mnoho průsečíků @b \left(k\cdot\frac\pi2,0\right), \ k\in\mathbb Z@b
Výraz má smysl, je-li definován @i\, \mathrm{tg}\, x\,@i a zároveň platí @i\, \cos^2x\neq0 @i. Obojí je splněno pro @b x \neq \frac{\pi}{2}+k\pi,\:k\in\mathbb{Z}.@b Pro tato @i\,x\,@i platí: @b \Bigl(\dfrac{\sin(2x)}{\cos^2 x}+2\mathrm{tg}^3\,x\Bigr)\cdot \sin\Bigl(\frac{3\pi}{4}\Bigr) = \biggl(\dfrac{\sin(2x)}{\cos^2 x}+2\Bigl(\dfrac{\sin x}{\cos x}\Bigr)^3 \biggr)\cdot \dfrac{\sqrt{2}}{2} =\biggl(\dfrac{2\sin x \cos x}{\cos^2 x}+\dfrac{2\sin^3 x}{\cos^3 x} \biggr)\cdot \dfrac{\sqrt{2}}{2} @b Použili jsme definici funkce tangens a vzorec pro sinus dvojnásobného úhlu. Dále zlomky sečteme (převedeme na společného jmenovatele) a použijeme Pythagorovu větu @i \,\sin^2x+\cos^2x=1@i. @b\biggl(\dfrac{2\sin x \cos x}{\cos^2 x}+\dfrac{2\sin^3 x}{\cos^3 x} \biggr)\cdot \dfrac{\sqrt{2}}{2} =\biggl(\dfrac{2\sin x \cos ^2x+2\sin^3 x}{\cos^3 x} \biggr)\cdot \dfrac{\sqrt{2}}{2}=\biggl(\dfrac{2\sin x (\cos ^2x+\sin^2 x)}{\cos^3 x} \biggr)\cdot \dfrac{\sqrt{2}}{2} =\dfrac{\sqrt{2}\sin x }{\cos^3 x} @b
Nesmíme dělit nulou a tangens je definován, je-li argument různý od @i\, \dfrac{\pi}{2}+k\pi@i. Musí být zároveň splněny podmínky @b\begin{array}{rcl}2-\sin x\neq0 &\wedge & 2x+\dfrac{\pi}{3} \neq \dfrac{\pi}{2}+k\pi\\[2mm] 2\neq \sin x& \wedge
& 2x \neq \dfrac{\pi}{6}+k\pi\\[2mm] x\in\mathbb R&\wedge & x\neq \dfrac \pi{12}+k\dfrac \pi2 \end{array}@b Funkce sinus nabývá hodnoty z intervalu @i\,\langle -1,1\rangle@i, proto nikdy nenabude hodnoty @i\,2@i. Druhá nerovnost představuje
vlastně nekonečně mnoho nerovností @i x \neq \dfrac{\pi}{12}+k\dfrac{\pi}{2},\ k\in \mathbb{Z}@i. Tedy @b \mathcal D(f) = \mathbb{R}\setminus\bigcup_{k\in\mathbb{Z}}\Bigl\{ \dfrac{\pi}{12}+k\frac{\pi}{2}\Bigr\}.@b
Nejprve určíme @i\,x\,@i z I. kvadrantu, pro které platí @b\cos x=\frac 12.@b Z tabulky víme, že @i\,x=\dfrac\pi 3@i. Kosinus nabývá záporných hodnot ve II. a III. kvadrantu. Dvě základní hodnoty jsou @b x_1=\pi-\frac \pi3=\frac 23\pi,\qquad\qquad x_2=\pi+\frac
\pi3=\frac 43\pi.@b Protože je funkce kosinus @i\,2\pi@i-periodická, bude mít rovnice nekonečně mnoho řešení @b x=\frac 23\pi+2k\pi \quad \vee\quad x=\frac 43\pi+2k\pi,\ k\in\mathbb Z,\\[2mm] K=\bigcup_{k\in\mathbb Z} \Bigl\{\dfrac 23\pi+2k\pi,
\dfrac 43\pi+2k\pi \Bigr\}.@b
Nejprve vyřešíme rovnici @b \mathrm{tg}\left(x+\dfrac \pi 3 \right)=\dfrac{\sqrt 3}3.@b Z tabulky víme, že tangens nabývá hodnoty @i\, \dfrac{\sqrt 3}3\,@i pro úhel @i\,\dfrac \pi 6@i a tangens je @i\,\pi@i-periodická funkce. Proto @b \begin{array} {rcl}
x+\dfrac \pi 3&=&\dfrac \pi 6+k\pi\\[2mm] x&=&-\,\dfrac \pi6+k\pi.\end{array}@b Nyní nakreslíme graf funkce @i\,f(x)= \mathrm{tg}\left(x+\dfrac \pi 3 \right)@i. Graf funkce tangens posuneme o @i\,\dfrac \pi 3\,@i jednotek ve směru osy
@i\,x\,@i doleva. Graf funkce @i\,f\,@i má svislé asymototy @i\,x=\dfrac\pi 6+k\pi,\ k\in\mathbb Z@i. Do stejného obrázku zakreslíme graf konstantní funkce @i\,g(x)=\dfrac {\sqrt 3}3@i, viz následující obrázek:
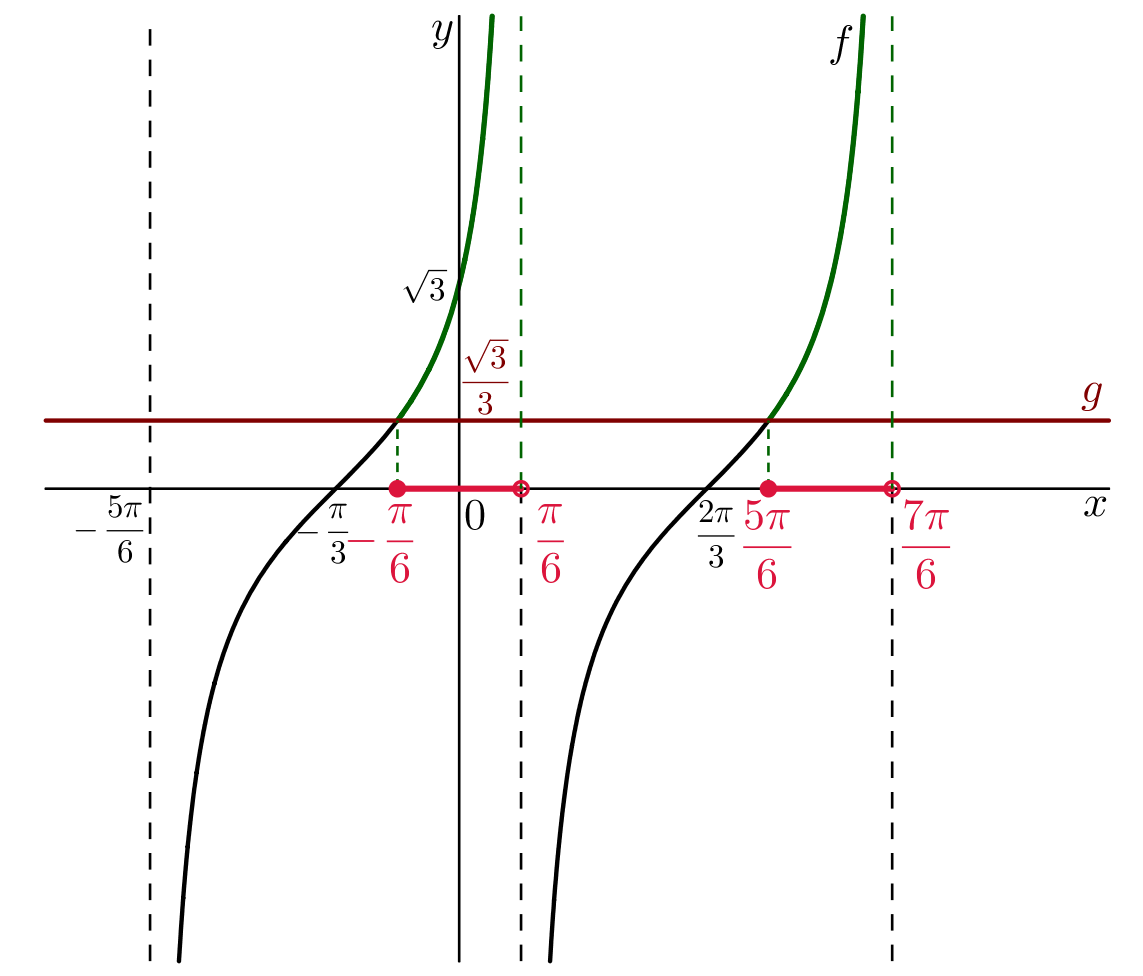
Máme spočtené @i\,x@i-ové souřadnice průsečíků grafů funkcí @i\,f\,@i a @i\,g@i. Z obrázku vidíme, že řešením dané nerovnice je sjednocení někonečně mnoho intervalů. @bK=\bigcup_{k\in\mathbb Z}\Big\langle -\,\dfrac\pi 6+k\pi,\frac \pi 6+k\pi\Big)@b
Neřešené příklady
- Řešte nerovnici @i\ \cos(2x-3)+\pi>0\,@i s reálnou neznámou @i\,x@i.
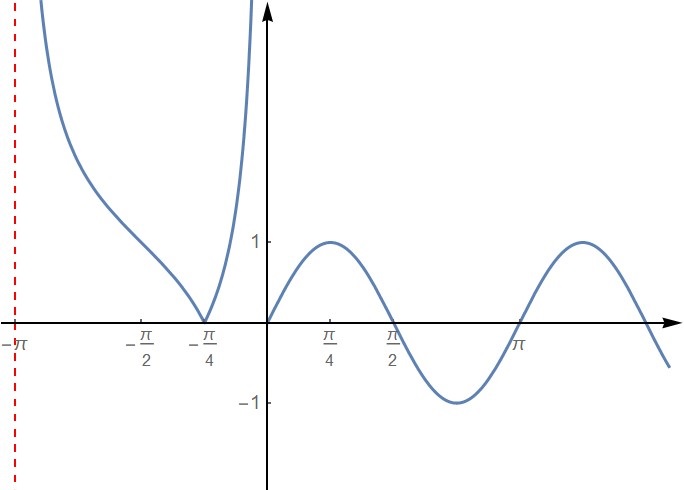
- Načrtněte graf funkce @i\ f(x) = \begin{cases}\bigl|1+\mathrm{cotg}(x)\bigr|,&x\in(-\pi,0),\\ \sin(2x),&x\geq 0.\end{cases}@i
- Určete definiční obor funkce @i\ f(x) = \sqrt{\cos x} @i.
- Graficky určete počet řešení rovnice @i\ 2\cos x = 1-\dfrac{2x}{\pi}.@i
- Určete, kdy má výraz @i\ \dfrac{1}{\sin\bigl(\frac{\pi}{6}\bigr)} + \dfrac{1-(\sin x + \cos x)^2}{\mathrm{cotg}\, x} \ @i smysl a upravte.

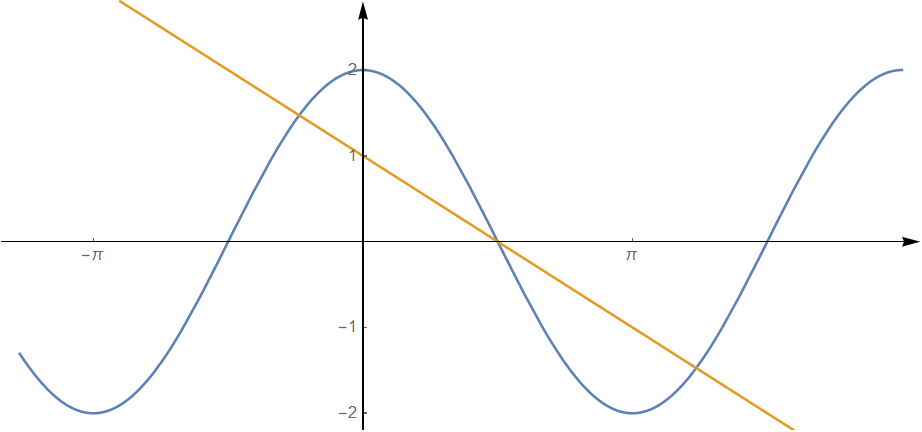 Rovnice má 3 řešení.
Rovnice má 3 řešení.