Absolutní hodnota, rovnice a nerovnice s absolutní hodnotou
Absolutní hodnota, rovnice a nerovnice s absolutní hodnotou

Teoretické minimum
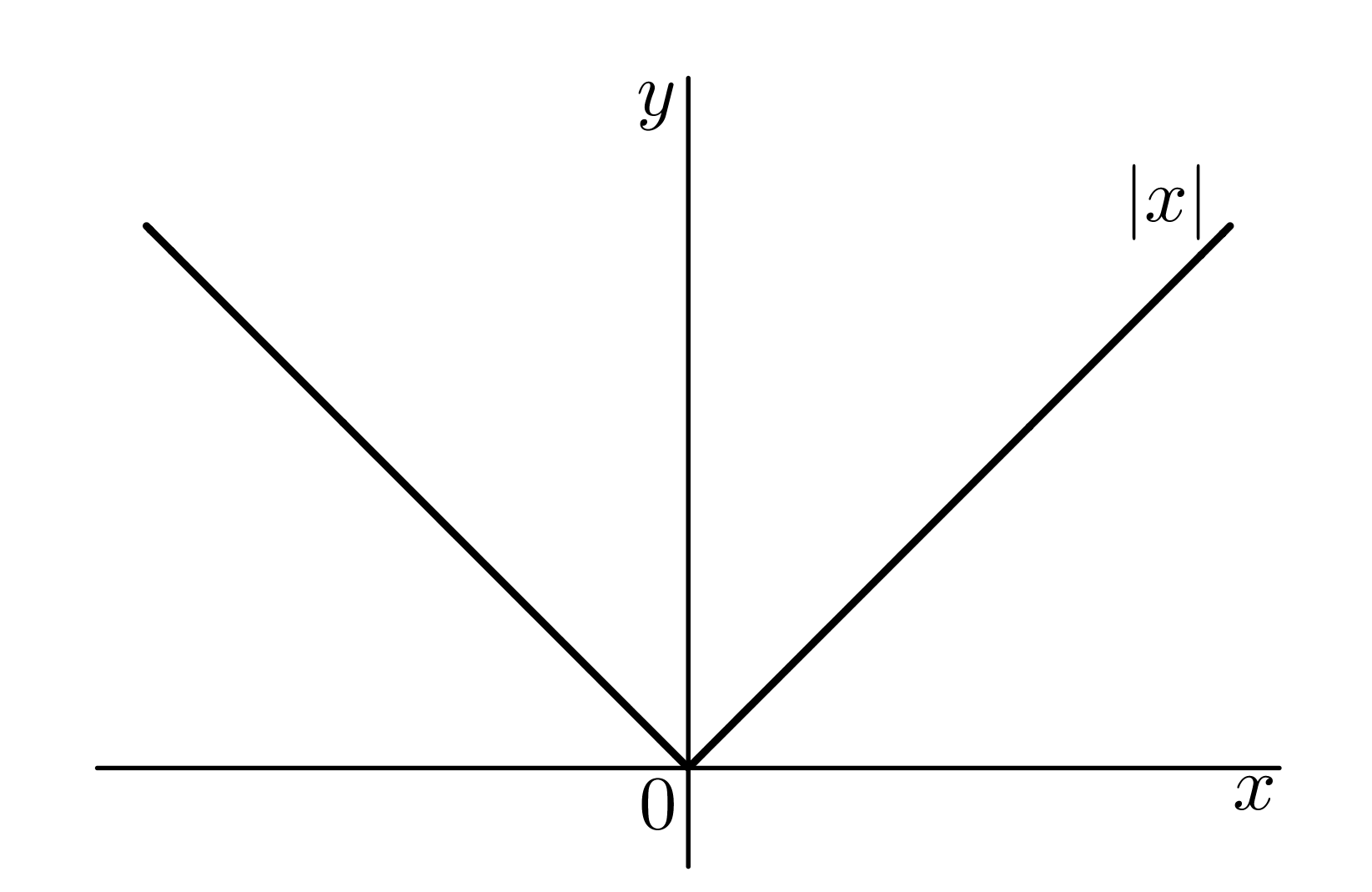
Absolutní hodnota je funkce daná předpisem @b f(x)=|x|.@b Absolutní hodnota je funkce, která nezápornému číslu přiřadí stejné číslo (identita @i\,y=x,\ x\geq0\,@i) a zápornému číslu přiřadí číslo opačné, tedy kladné ( @i\,y=-x,\ x<0\,@i). Definičním oborem jsou všechna reálná čísla, tj. @b\mathcal D(f)=\mathbb R @b a oborem hodnot všechna nezáporná čísla, tj. @b\mathcal H(f)=\langle 0,\infty).@b Graf se skládá ze dvou polopřímek, viz obrázek:
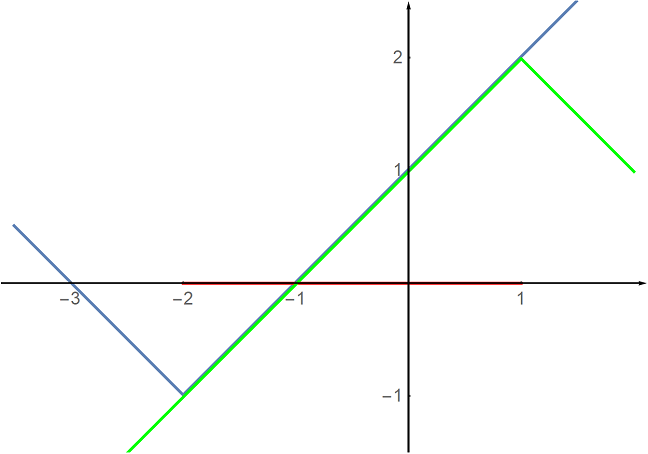
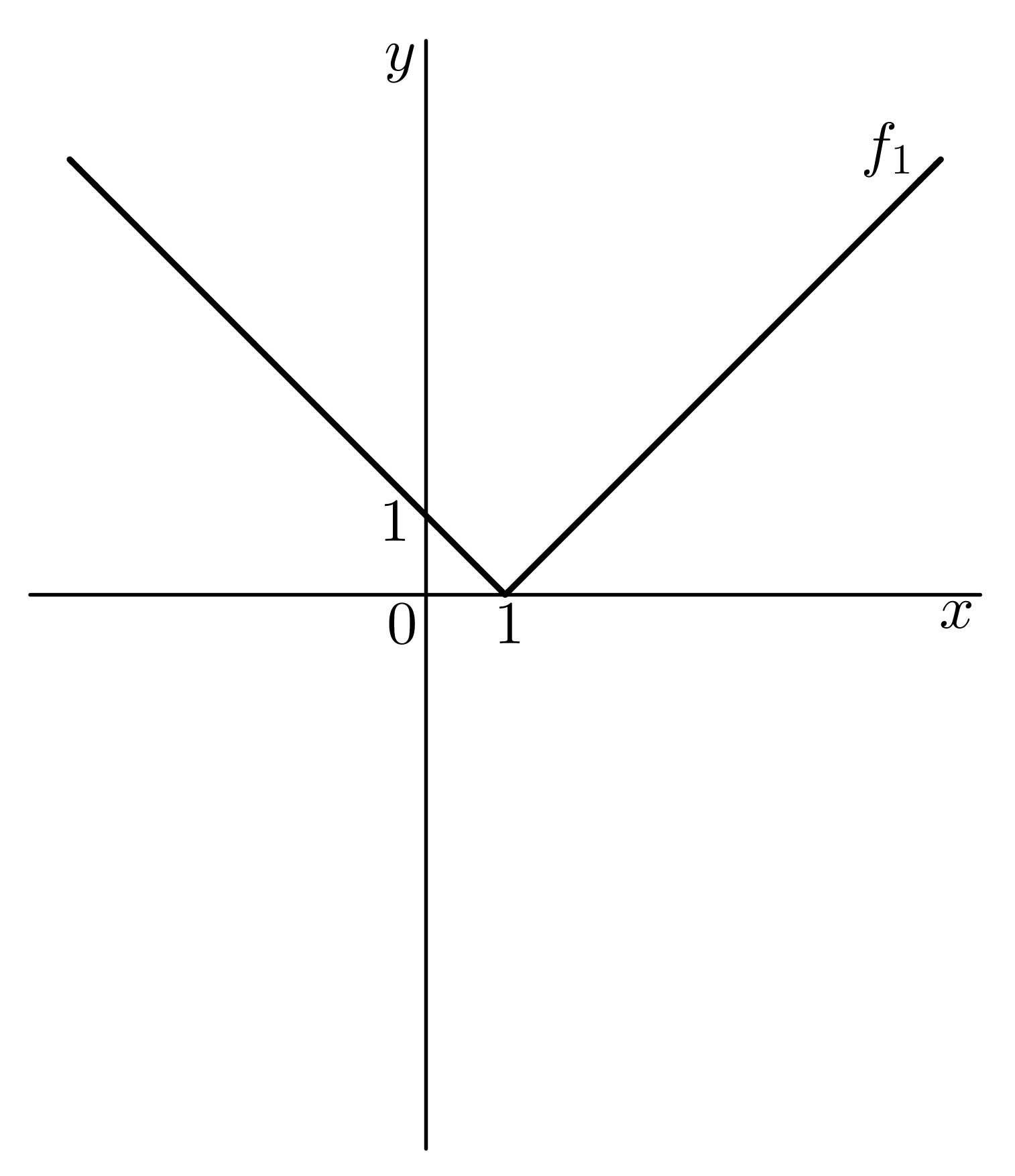
Nakresleme graf funkce @i\,f(x)=2-|1-x|\,@i a určeme její obor hodnot. Postupně nakreslíme grafy funkcí @i\, f_1(x)=|1-x|=|x-1|,\ f_2(x)= -|1-x|\,@i
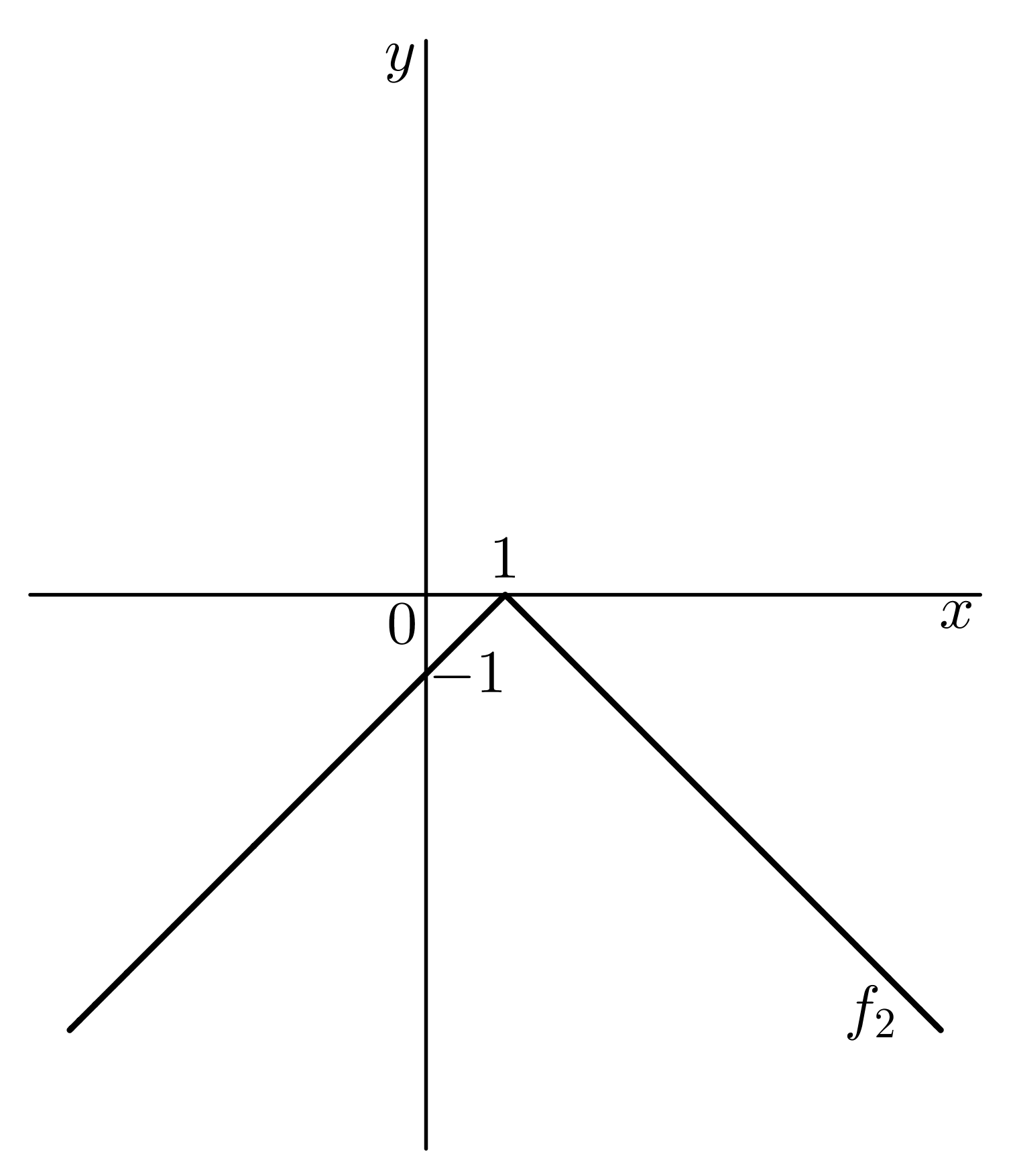
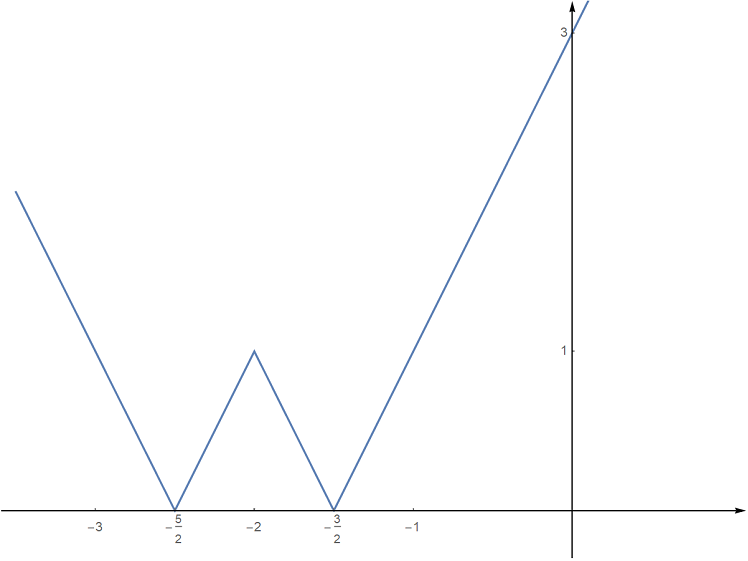
a nakonec graf funkce @i\,f(x)=2-|1-x|@i:
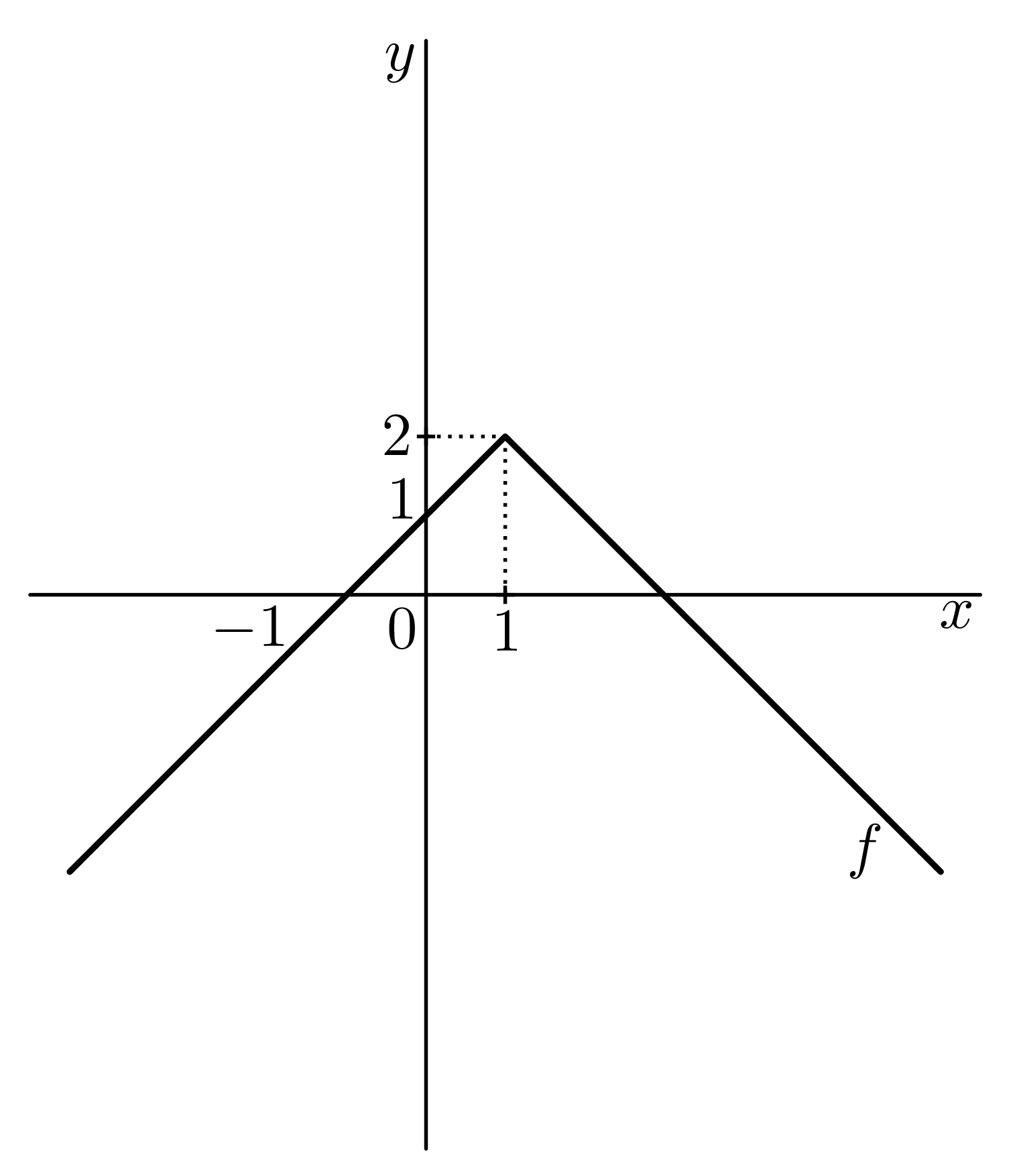
Z obrázku vyčteme, že @i\mathcal H(f)=(-\infty,2\rangle @i.
Související
Nerovnice s absolutní hodnotou, graf funkce.
Řešené příklady
- Řešte rovnici @i\, |x+3| = 10\,@i pro reálnou neznámou @i\,x@i.
- Řešte rovnici @i \, 1-|x+1| = |3-x|\,@i pro reálnou neznámou @i\,x@i.
- Načrtněte graf funkce @i \,f(x) = \bigl|\sqrt{|x|}-1\bigr|@i.
- Určete graficky počet řešení rovnice @i\,|3-2x|+|x|-2=0@i.
- Řešte graficky nerovnici @i \, |x^2-2x| \geq 1-2\sqrt{x-1}@i.
Víme, že absolutní hodnota čísla @i10@i a @i-10@i je rovna hodnotě @i10@i. Tedy @b\begin{array}{rclcrcl}x+3&=&10&\qquad \vee\qquad &x+3&=&-10\\[2mm] x&=&7 &\qquad\vee\qquad &x&=&-13.\end{array} @b Rovnice má dvě řešení, tj. @bK=\{-13, 7\}.@b
Užitečná poznámka: Přepišme rovnici na tvar @i\,|x-(-3)|=10@i. Geometrický význam rovnice je následující: Úloha najít reálná čísla @i\,x@i, pro která platí, že vzdálenost jejich obrazů od obrazu čísla @i\,-3\,@i na reálné ose je @i\,10@i.
1. způsob řešení - analyticky pomocí metody nulových bodů. Rovnici budeme řešit zvlášť na intervalech, kde mají výrazy v absolutní hodnotě konstantní znaménko. Nulové body výrazů s absolutní hodnotou jsou @i\, x_1=-1, \ x_2=3@i. Proto množinu reálných čísel rozdělíme na podintervaly: @i\,\mathbb R=(-\infty,-1)\cup\langle -1,3\rangle\cup(3,\infty)@i.
Pro @i\, x\in(-\infty,-1)\,@i platí @i\, x+1< 0\,@i a @i\, 3-x> 0 @i, a tedy @i\, |x+1| = -(x+1)@i, resp. @i\,|3-x| = 3-x.@i Odstraněníme absolutní hodnoty v rovnici na uvedeném intervalu a rovnici vyřešíme:
@b \begin{array}{r c l} 1- \bigl(-(x+1)\bigr)&= &3-x\\
x+2&= &3-x\\
2x&= &1\\ x&=&\frac 12. \end{array}@b
Řešení @i \, x=\frac{1}{2} \,@i neleží v uvažovaném intervalu @i\, (-\infty,-1)\,@i, není tedy řešením původní rovnice.
Podobně na intervalu @i\,\langle -1,3 \rangle\,@i máme @i\,|x+1| = x+1\,@i a @i\,|3-x| = 3-x.@i @b \begin{array}{r c l} 1-(x+1)&= &3-x\\ -x &= &3-x\\ 0 &\neq &3. \end{array}@b
A konečně na intervalu @i (3,\infty)@i je @i\,|x+1| = x+1\,@i a @i\,|3-x| = -(3-x).@i Dostáváme @b \begin{array}{r c l} 1-(x+1)&= &-(3-x)\\ -x &= &-3+x\\ 2x &= &3\\ x &= &\frac32\notin(3,\infty) . \end{array}@b Rovnice nemá řešení, tj. @i\,K=\emptyset.@i
2. způsob řešení - graficky. Načrtneme grafy funkcí @i y=1-|x+1|@i, @i y=|3-x|@i .
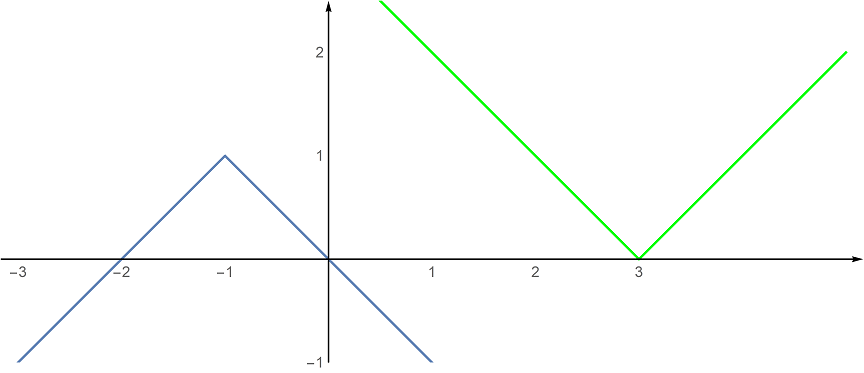
Počet řešení odpovídá počtu průsečíků obou grafů, grafy se neprotínají. Rovnice nemá řešení.
Výsledný graf získáme postupnými transformacemi základního grafu funkce @i \,f_1(x) = \sqrt{x}@i.
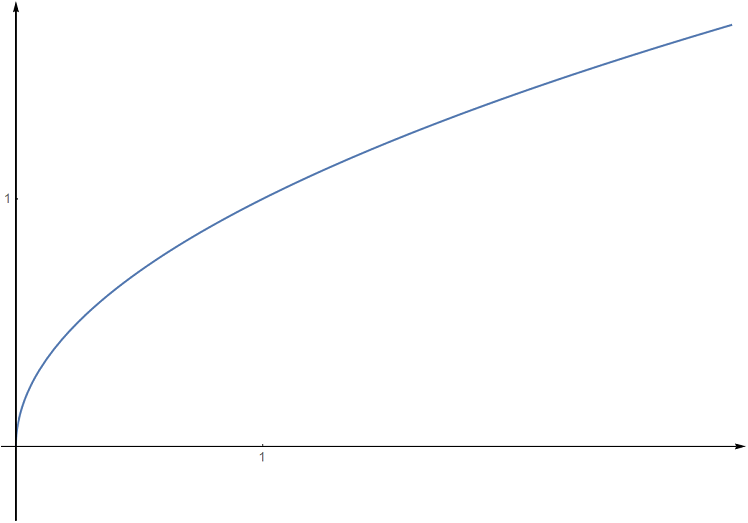
Funkce @i\,f_2(x) = \sqrt{|x|}\,@i je definována pro všechna @i\, x \in\mathbb{R}\,@i a je sudá (@i\,\sqrt {|x|}=\sqrt{|-x|}\ @i)-graf je symetrický podle osy @i\,y@i, přičemž pro @i\, x\geq 0\, @i platí @i\, f_2(x) = f_1(x).@i
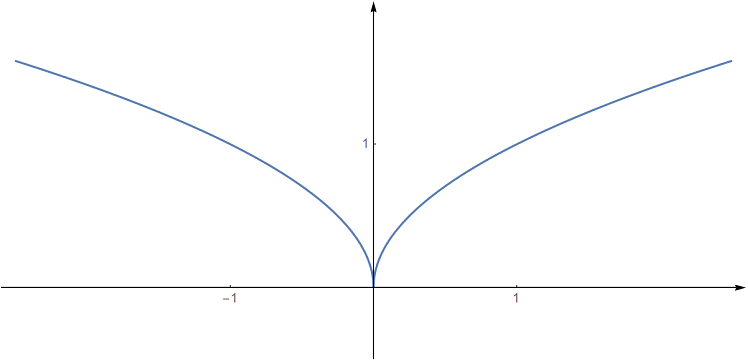
Funkční hodnoty funkce @i\,f_3(x) = \sqrt{|x|}-1\,@i jsou o jedna menší než pro @i\,f_2@i:
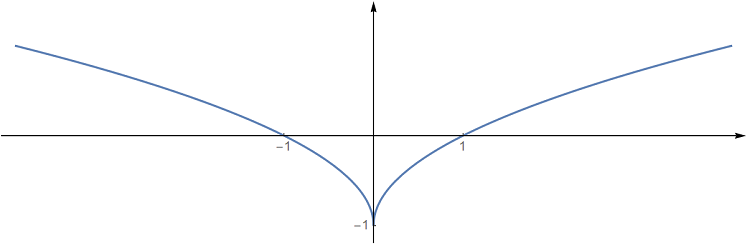
Funkční hodnoty funkce @i\,f(x) =| \sqrt{|x|}-1|\,@i jsou nezáporné, graf musí ležet nad osou @i\,x@i. Část grafu nad osou @i \,x\, @i se nezmění, část pod osou @i\, x\, @i se symetricky podél osy @i\,x\,@i překlopí do kladných hodnot (nad
osu @i\, x @i). Výsledný graf funkce @i\,f\,@i je na následujícím obrázku.
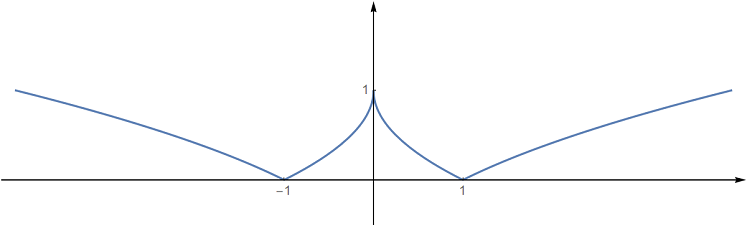
Rovnici přepíšeme do takového ekvivalentního tvaru, abychom uměli snadno načrtnout graf funkce na levé i pravé straně rovnice. @b 2\cdot\left|\frac{3}{2}-x\right|=2-|x| @b Počet řešení odpovídá počtu průsečíků grafů funkcí @i\, y =2\cdot\Bigl|\frac{3}{2}-x\Bigr|\,@i
a @i\,y=2-|x|.@i
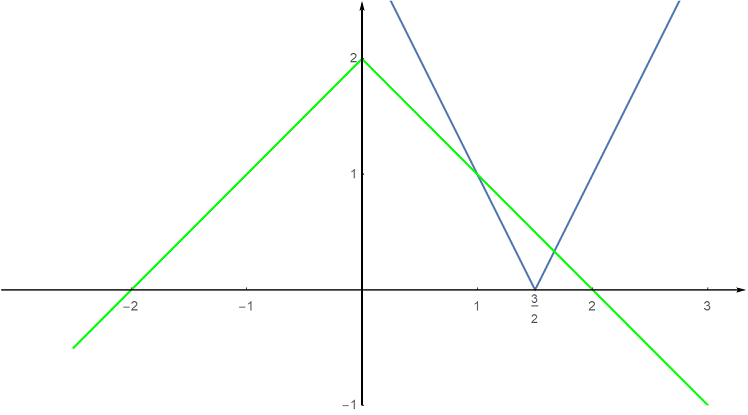
Rovnice má dvě řešení.
Užitečná poznámka: Co se týče přesné hodnoty obou řešení - odpovídají @i\,x@i-ovým souřadnicím průsečíků v obrázku. Z obrázku je zřejmá hodnota prvního z nich @i\,x_1 = 1@i. Dále z obrazku vyčteme, že druhé řešení leží v intervalu @i\,(\frac{3}{2},2)@i. Na tomto intervalu dostáváme odstraněním absolutních hodnot v rovnici : @b \begin{array}{r c l} |3-2x|&=&2-|x|\\ -(3-2x)&= &2-x\\-3+2x&= &2-x\\3 x&= & 5 \\x_2&= &\frac53\in\left(\frac 32,2\right). \end{array}@b druhé řešení. Tedy @bK=\Bigl\{ 1,\frac53 \Bigr\}.@b
Označme funkci na levé straně nerovnice písmenkem @i\,f@i, tj. @i\, f(x)= |x^2-2x|\,@i a funkci na pravé straně písmenkem @i\,g@i, tj. @i\,g(x)=1-2\sqrt{x-1} @i. Do jednoho obrázku zakreslíme graf funkce @i\,f\,@i a graf funkce @i\,g@i. Graf funkce @i\,f\,@i získáme z paraboly @i\,y=x^2-2x@i, která protíná osu @i\,x\,@i v bodech @i\,x_1=0,\ x_2=2@i. Část paraboly, která leží pod osou @i\,x@i, překreslíme symetricky nad osu @i\,x@i. Grafem funkce @i\,g\,@i je druhá odmocnina posunutá o jedničku doprava ve směru osy @i\, x@i, následně je překlopená kolem osy @i\,x@i. Násobek dvojkou nezmění kvalitu grafu, funkční hodnoty se budou měnit dvakrát rychleji. Nakonec odmocninu posuneme o jedničku nahoru ve směru osy @i\,y@i, graf funkce @i\,g\,@i vychází z bodu@i\,(1,1)@i, viz obrázek:
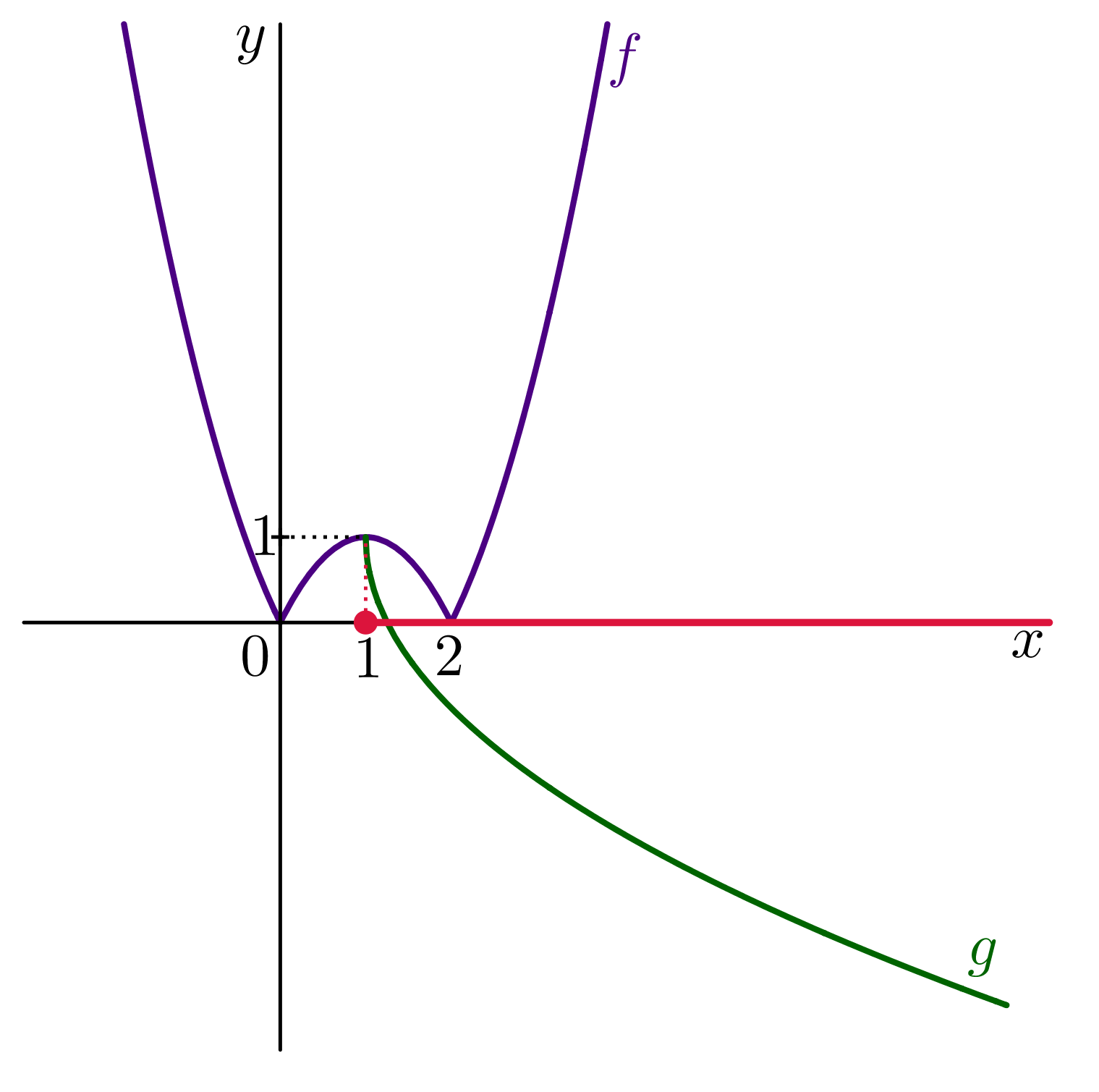
Z obrázku je patrné, že @i\,f(x)\geq g(x)\,@i pro všechna @i\,x\in\langle 1,\infty)@i. Tedy řešením nerovnice je interval @i\,K=\langle 1,\infty)@i.
Užitečná poznámka: @ix@i-ová souřadnice průsečíku grafu funkce @i\,g \,@i s osou @i\,x\,@i je kořenem rovnice @i\,1-2\sqrt{x-1}=0@i. Rovnice má jedno řešení @i\,x=\frac 54@i.
Neřešené příklady
- Řešte v @i\,\mathbb R\,@i rovnici @i\,|x^2-2|+x=0.@i
- Řešte v @i\,\mathbb R\,@i rovnici @i|x+2|-1 = 2-|x-1|.@i
- Načrtněte graf funkce @i\,f(x) =\bigl|1-|4+2x|\bigr|.@i