Logo OP VVV

Teoretické minimum

Kuželosečky (kružnice, elipsa, parabola a hyperbola) jsou rovinné křivky. Lze je zavést několika způsoby. Jednou z možností je jako průnik kuželové plochy s rovinou. Průnikem může být (kromě bodu, přímky, či dvojice přímek) buď kružnice, elipsa, parabola nebo hyperbola, viz následující obrázky. Odtud také název kuželosečky.



My se v dalším omezíme na popis kuželoseček pomocí rovnic. V kartézské souřadnicové soustavě budeme uvažovat pouze kuželosečky, které mají osu rovnoběžnou s osou @ix@i nebo osou @iy@i. Takové kuželosečky lze popsat rovnicí

@i A{x^2} + B{y^2} +C x + D y +E =0 \ , @i

kde @iA,B,C,D,E@i jsou reálné konstanty.


Podle konstant @iA,B,C,D,E@i se naučíme poznat, jakou kuželosečku rovnice představuje, a tuto kuželosečku nakreslit.

Poznámka: Uvědomte si, že na dané kuželosečce leží právě ty body, které vyhovují její rovnici, viz první řešený příklad níže.

Uvedeme vždy nejprve rovnici kuželosečky, kdy střed, resp. vrchol je umístěn do počátku. Tu také znázorníme na obrázku. Následně pak uvedeme rovnici, kdy kuželosečka je posunuta tak, že střed, resp. vrchol je posunut do bodu @i({x_0},{y_0})@i. Při určování tohoto posunutí v konkrétních příkladech obvykle využíváme tzv. doplnění na čtverec.

Rovnice kružnice

Kružnice se středem v počátku a poloměrem @ir>0@i je popsána rovnicí

@i x^{2} + y^{2} = {r^2}\ , @i



Kružnice se středem @iS=({x_0},{y_0})@i a poloměrem @ir>0@i je popsána rovnicí

@i (x-{x_0})^{2} + (y-{y_0})^{2} = {r^2}\ . @i

Poznámka: Je-li @i A {x^2} + B {y^2} + C x + D y +E =0@i rovnicí kružnice, je nutně @iA=B \neq 0@i.

Poznámka: Výraz @i\sqrt{ (x-{x_0})^{2} + (y-{y_0})^{2}}@i odpovídá eukleidovské vzdálenosti bodu @iX = (x,y)@i a @i S=(x_0,y_0)@i. Body ležící na kružnici jsou tedy právě body o souřadnicích (x,y), které jsou vzdáleny od středu kružnice @iS@i o @i r@.i

Rovnice elipsy

Elipsa se středem v počátku a poloosami @ia>0@i, @ib>0@i, @ia\neq b@i, je popsána rovnicí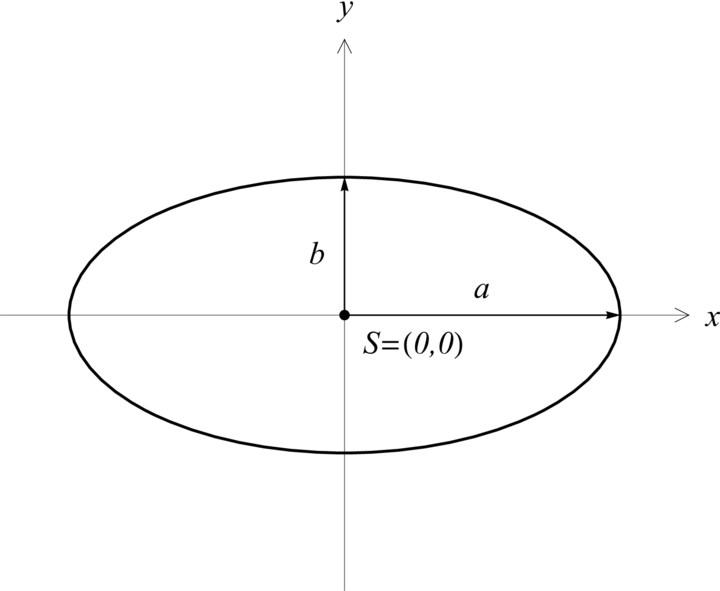

@i \dfrac{x^{2}}{a^2} + \dfrac{y^{2}}{b^2} = 1\ , @i


Elipsa se středem @iS=({x_0},{y_0})@i a poloosami @ia>0@i, @ib>0@i, @ia\neq b@i, je popsána rovnicí

@i \dfrac{(x-{x_0})^{2}}{a^2} + \dfrac{(y-{y_0})^{2}}{b^2} = 1. @i

Je-li @iA{x^2} + B{y^2} +C x + D y +E =0@i rovnicí elipsy, je nutně @iA,B \neq 0@i, @iA \neq B@i a čísla @iA@i a @iB@i mají stejná znaménka.

Rovnice paraboly

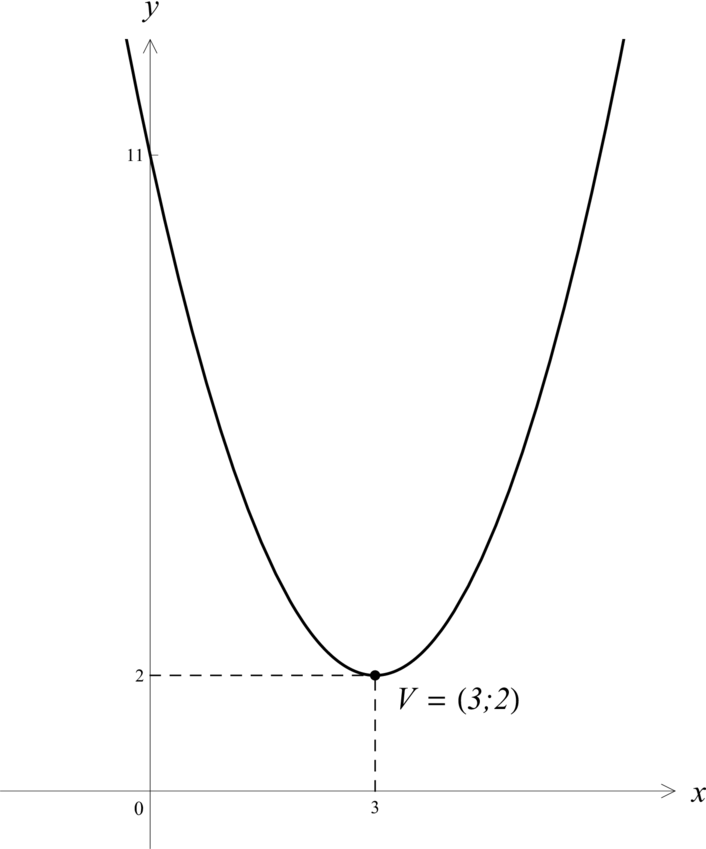
Parabola s vrcholem v počátku a osou totožnou s osou @iy@i je popsána rovnicí

@i y= a x^{2}\ , a \neq 0\ . @i

Parabola s vrcholem @iV=({x_0},{y_0})@i a osou rovnoběžnou s osou @iy@i je popsána rovnicí

@i y-{y_0}= a (x-{x_0})^{2}\ , a \neq 0\ . @i

Parabola s vrcholem v počátku a osou totožnou s osou @ix@i je popsána rovnicí

@i x= a y^{2}\ , a \neq 0\ . @i

Parabola s vrcholem @iV=({x_0},{y_0})@i a osou rovnoběžnou s osou @ix@i je popsána rovnicí

@i x-{x_0}= a (y-{y_0})^{2}\ , a \neq 0\ . @i

Znaménko čísla @ia@i rozhoduje v obou případech o orientaci paraboly, jak je patrné z následujících obrázků.



Je-li @iA{x^2} + B{y^2} +C x + D y +E =0@i rovnicí paraboly, je nutně jedno z čísel @iA@i nebo @iB@i rovno 0 a druhé nenulové. Je-li @iA=0@i a @iB\neq 0@i, je osa paraboly rovnoběžná s osou @ix@i, je-li @iB=0@i a @iA\neq 0@i, je osa paraboly rovnoběžná s osou @iy@i.

Rovnice hyperboly

Hyperbola se středem v počátku a poloosami @ia>0@i, @ib>0@i a hlavní osou (tj. přímkou procházející jejími vrcholy) totožnou s osou @ix@i je popsána rovnicí

@i \dfrac{x^{2}}{a^2} - \dfrac{y^{2}}{b^2} = 1\ . @i

Hyperbola se středem @iS=({x_0},{y_0})@i a poloosami @ia>0@i, @ib>0@i a hlavní osou rovnoběžnou s osou @ix@i je popsána rovnicí

@i \dfrac{(x-{x_0})^{2}}{a^2} - \dfrac{(y-{y_0})^{2}}{b^2} = 1\ . @i

Hyperbola se středem v počátku a poloosami @ia>0@i, @ib>0@i a hlavní osou totožnou s osou @iy@i je popsána rovnicí

@i \dfrac{y^{2}}{b^2}-\dfrac{x^{2}}{a^2} = 1\ . @i

Hyperbola se středem @iS=({x_0},{y_0})@i a poloosami @ia>0@i, @ib>0@i a hlavní osou rovnoběžnou s osou @iy@i je popsána rovnicí

@i \dfrac{(y-{y_0})^{2}}{b^2}-\dfrac{(x-{x_0})^{2}}{a^2} = 1\ . @i

 

Je-li @iA{x^2} + B{y^2} +C x + D y +E =0@i rovnicí hyperboly, je nutně @iA,B \neq 0@i a čísla @iA@i a @iB@i mají různá znaménka. 


Řešené příklady

  1. Rozhodněme, které z bodů @iA=(0,-3),\ B=(2, \sqrt{5}), \ C=(3,1)@i leží na kružnici popsané rovnicí @ix^2 + y^2=9@i.

    2. Souřadnice bodu @iA@i splňují: @i0^2 + 3^2 =9@i, tedy bod @iA@i náleží dané kružnici. Bod @iB@i: @i2^2 + {\sqrt{5}}^2 =9@i, podobně tedy i bod @iB@i náleží dané kružnici. Bod @iC@i: @i3^2 + 1^2 =10 \neq 9@i, tedy bod @iC@i nenáleží dané kružnici.
  2. Ukažme, že rovnice @i 2x^{2} +10 + 2y^{2} +12y=0 @i je rovnicí kružnice. Určeme střed a poloměr této kružnice.

    3. Nejprve rovnici vydělíme dvěma. Dostaneme

    @i x^{2} +5 + y^{2} +6y=0. @i

    Jak jsme již uvedli, základní metodou je doplnění na čtverec. To se v našem případě týká proměnné @iy@i. Konkrétně členy @iy^{2} +6y@i chceme doplnit o vhodnou konstantu @iC@i tak, aby @iy^{2} +6y+C = (y+K)^2@i pro nějaké K. Konstantu @iC@i je pak samozřejmě nutné opět odečíst, abychom dostali ekvivalentní rovnici. Postupně tedy upravujeme takto:

    @i x^{2} +5 + y^{2} +6y=0 @i

    @i x^{2} + y^{2} +6y=-5 @i

    @i x^{2} + (y^{2} +6y +9) -9=-5 @i

    @i x^{2} + (y+3)^2 -9=-5 @i

    @i x^{2} + (y+3)^2 =4 @i

    Z tohoto tvaru již vidíme, že se jedná o rovnici kružnice se středem v bodě @iS=(0,-3)@i a poloměrem @ir=2@i.
  3. Ukažme, že rovnice @i x^{2} -2x + 4y^{2} +8y=-1 @i je rovnicí elipsy. Určeme střed a poloosy této elipsy.

    4. Opět je základní metodou doplnění na čtverec. Postupně tedy upravujeme rovnici takto:

    @i x^{2} -2x + 4y^{2} +8y=-1 @i

    @i (x^{2} -2x +1) + (4y^{2} +8y +4) =-1 +1+4 @i

    @i (x-1)^{2} + 4(y+1)^{2} =4 @i

    @i \frac {(x-1)^{2}}{4} + (y+1)^{2} =1 @i

    Z tohoto tvaru již vidíme, že tato rovnice je rovnicí elipsy se středem @iS=(1,-1)@i a poloosami @ia=2@i a @ib=1@i
  4. Určeme a nakresleme kuželosečku popsanou rovnicí @i 2x + {y^2} +4y -6= 0@i.

    5. Po doplnění na čtverec dostáváme

    @i 2x + ({y^2} +4y +4) -4 -6= 0@i

    @i 2x + (y+2)^2 -10= 0@i

    @i 2x -10 = -(y+2)^2@i

    @i x -5 = - \frac 12 (y+2)^2@i

    Což je rovnice paraboly s vrcholem @iV=(5,-2)@i a osou rovnoběžnou s osou @ix@i.


  5. Nakresleme kuželosečku popsanou rovnicí @i {x^2}={4y^2}-4x -8y -4.@i

    6. Nejprve převedeme všechny lineární i kvadratické členy na levou stranu rovnice a z členů obsahujících @iy@i vytkneme @i-4@i, tím získáme ekvivalentní rovnici @i x^2 +4x -4(y^2 -2y) =-4.@i Po doplnění na čtverec pak @i (x^2 +4x +4) -4 -4(y^2 -2y +1) +4 =-4,@i @b (x+2)^2 -4(y-1)^2 =-4.@b Nyní vydělíme celou rovnici @i4@i: @i \frac {(x+2)^2}{4} -(y-1)^2 =-1,@i a vynásobíme @i(-1)@i: @i (y-1)^2 -\frac {(x+2)^2}{4} =1.@i Z tohoto tvaru rovnice již vidíme, že se jedná o rovnici hyperboly se středem v bodě v bodě @iS=(-2,1)@i, s poloosami @ia=2@i a @ib=1@i a s hlavní osou rovnoběžnou s osou @iy@i (je to přímka @ix=-2@i). Hyperbola je nakreslena na následujícím obrázku.

  6. Určete průsečíky kružnice se středem v bodě @iS = (1,-2)@i a poloměrem @ir=2@i s osou @i y@i.

    7. Rovnicí dané kružnice je @i (x-1)^2 + (y+2)^2 = 4. @i Pro průsečíky s osou @i y @i máme @i x=0,@i odkud @b (-1)^2 + (y+2)^2 = 4 @b a @iy= -2 \pm \sqrt{3}@i. Kružnice má tedy s osou @i y @i dva průsečíky @iP_1 = (0,-2+\sqrt{3})@i, @iP_2 = (0,-2-\sqrt{3}).@i

Neřešené příklady

  1. Převeďte @ix^{2} -2x + y^{2} +4y=4@i na rovnici kružnice v základním tvaru a z něj určete střed a poloměr této kružnice.
  2. Nakreslete kuželosečku zadanou rovnicí @i y+6x=x^2+11. @i
     
  3. Popište kuželosečku o rovnici @i 2x^2 + y^2 = 2( y +1 ) + x^2@i.
  4. Popište kuželosečku o rovnici @ix^2 + 2y^2 + 8 = 4 (2y-x)@i.
  5. Určete průsečíky přímky @i y= x+2@i s elipsou se středem v bodě @i S = (1,2)@i a délkami poloos @i a=1 @i a @ib=2.@i

Licence CC BY

Last modified: Wednesday, 8 June 2022, 2:10 PM
◄ Příklady k procvičování - rovnice přímky
Příklady k procvičování - kuželosečky ►